Wiskundige problemen en probleempjes 2

[lotte]

natuurlijk oomski
'k zit hier ook "toeme" te zeggen
maar dan om een andere reden

1% = 100
97% rode ballen = 9700

[pastoor]

Vraag 2, wat een reactie.

Er zijn 30000 ballen (1% blauwof 300, 99% rood of 29700). Men neemt rode ballen "tot er in het nieuwe totaal nog 97% rode ballen zijn".

Ik dacht eerst, even het impact bekijken met " er 10000 weg te nemen", maar ik heb het niet gedaan, want de oplossing staat in de opgave. Want 3% (=300) is blauw, en 97% (dus 9700) = rood. Men moet dus 20000 ballen wegnemen.

Meester Denook schreef:
"We halen er enkele rode ballen uit".
maar hij wist veel beter.

[oomski]

ja, zo zag ik het ook.

Op een totaal van 10000 is 300 blauwe en 9700 rode toch 3% en 97% ?
dus er zijn 20000 rode ballen weggenomen om aan die % te komen. Niet?

[denook]

goede avond iedereen,

beginnen we aan een eerste evaluatie ...

vraag 8 ) lotte - ok.

dit was een vraagje dat ook al eens buiten de wiskunde opduikt.
Bedoeling is dat de cijferaar de benen van de buschauffeur vergeet.
Lotte doet dat natuurlijk niet.

vraag 2) pastoor - ok - later bevestigd door oomski

wat valt op? lotte en pastoor postten in dezelfde minuut.
Pastoor is slim; hij geeft alleen het antwoord, geen berekeningen -
waren niet expliciet gevraagd - en zo was zijn typwerk vlugger klaar
dan dat van lotte ...
De uitleg kort (-oomski en lotte gingen er ook al voor in de pen-):
30000 ballen - 1% blauwe, geeft 300 blauwe ballen.
De 300 blauwe ballen blijven, doch zijn nu 3% van het totaal.
3% is 300,
1% is 100
97% is 9700; dus 9700 rode ballen

vraag 6) sloeberkebebo - ok

er werd gevraagd: 'BEREKEN' de afstand ...
maar, zeker voor sloeberkebebo, volstaat hier een figuur + meten.
Let op, voor allen die alleen tekenen: het antwoord was hier exact
3 meter. Was het antwoord 'wortel5' geweest, dan zou sloeberkebebo
zeker een komma-getal hebben gevonden en de beredeneerders de
echte waarde 'wortel5'.
Tussendoor geef ik wel eens de formule voor dit probleem - het is
een mooie formule, zonder welke je hier niet verder kan.

vraag 4) - troontje - ok - weer met akkoord door oomski.

Vier vragen opgelost - blijven er dus zes.

Beste Oomski, er rest nog een typische oomski-vraag.
Pik ze er uit en post ze als eerste.

tot morgen iedereen,

denook

[lotte]

Goeie avondwens voor iederéén

10) Ik zet achteraan een getal een ‘nul’ bij. Zo wordt het oorspronkelijke getal vermeerderd met 1107. Wat was het oorspronkelijke getal?

antwoord : 1230

lotte.

[sloeberkebebo]

Beste allemaal ,

Ik denk dat wij voor dit voorbeeld ( vraag 6 ) met deze gegeven maten , de diagonaal van deze rechthoek is gewoon gelijk aan de radius van de cirkel .



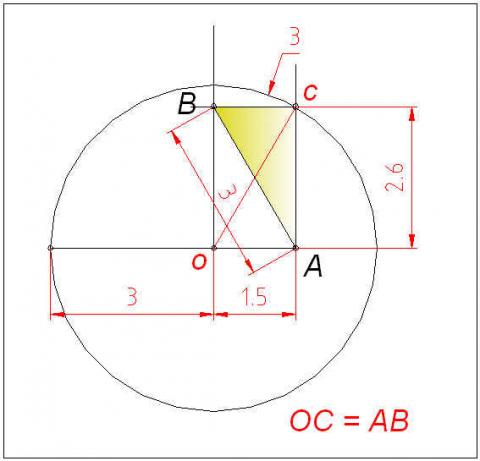
Groetjes

Sloeber

[lotte]

dubbele posting, sorry
lotte.

[pastoor]

Goede avond allemaal.

Vraag 9) Men vormt een rij getallen met als eerste term 4² en als tweede term 2-tot de macht4. De derde term is het quotiënt van de eerste en de tweede term. De vierde term is het quotiënt van de tweede en de derde term; en zo verder. Als we de tien eerste termen van de rij met elkaar vermenigvuldigen, waaraan is het product dan gelijk?

De eerste is (4²) = (2(macht 4)).
De tweede is (2²*2²) = (2(macht 4)).
De derde is (1ste/2de) = (2(macht 4))/(2(macht 4)) = 1.
De vierde is (2de/3de) = (2(macht 4))/1 = (2(macht 4)).
De vijfde is (3de/4de) = 1/(2(macht 4)) = (2(macht -4)).
De zesde is (4de/5de) = (2(macht 4))/(2(macht -4)) = (2(macht 8 )).
Het 7de is (5de/6de) = (2(macht -4))/(2(macht 8 )) = (2(macht -12).
Het 8ste is (6de/7de) = (2(macht 8 ))/(2(macht -12)) = (2(macht 20)).
Het 9de is (7de/8ste) = (2(macht -12)/(2(macht 20)) = (2(macht -32)).
Het 10de is (8ste/9de) = (2(macht 20))/(2(macht -32)) = (2(macht 52)).

Het product is van de tien eerste termen is:
(2(macht (4+4+4-4+8-12+20-32+52))) =
(2(macht 44)) = (4(macht22) = (4*(8(macht 14))) = (16(macht 11))

[pastoor]

eh

[sloeberkebebo]

Goede avond allemaal



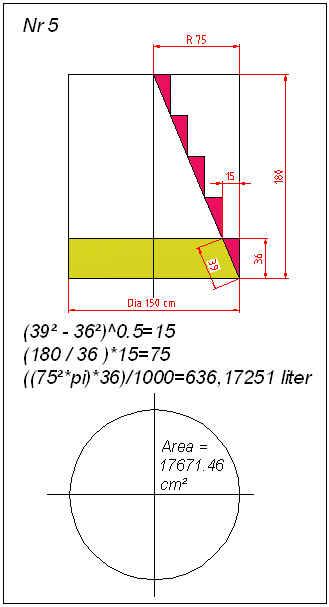
Groetjes Sloeber

[lotte]

"pastoor"

Voor vraag 10 heb ik eentweedrie (123) als oplossing,
het oorspronkelijke getal. Tikfout.
Oorspronkelijke getal is A.
Dan is (A + 1107) = 10A of 1107= 10A – A of 9A = 1107 of A = 123

Pastoor,
détails, détails, détails
lotte.

[oomski]

Goedenavond allen.

Vraag 1:
90° + 57,33° = 147,33°
180° - 147,33° = 32,67°
of
90° - 57,33° = 32,67°

[sloeberkebebo]

Lieve Oomski ,

Volgens mij bent U verkeerd ! ( Vraag 1 )
57°33'===>>57,55°
90°-57,55°=32,45° ===>> 32°27'

1° = 60'

Hoek B=32°27' of 32,45°



Groetjes Sloeber

[oomski]

Klopt Sloeberkebo, ik heb die minuut aan 100 geteld. het moet idd 32°27' zijn; Dank u.

[troontje]

goede middag iedereen,


niet gezien dat vraag reeds opgelost was door sloeberkebebo

troontje,