Wiskundige problemen en probleempjes 2
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Vraag 6
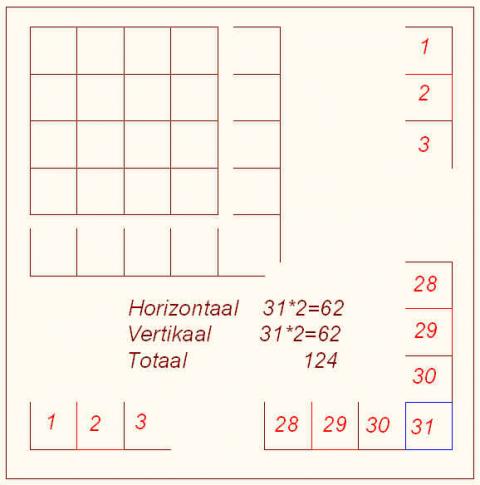
Hoeveel lucifers heeft vierkant 31 meer dan 30?
Nog eens nagezien , 124 lucifers
Groetjes
Sloeber

Hoeveel lucifers heeft vierkant 31 meer dan 30?
Nog eens nagezien , 124 lucifers
Groetjes
Sloeber
Laatst gewijzigd door sloeberkebebo op 26 nov 2009, 10:49, 1 keer totaal gewijzigd.
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
vlug een evaluatie, want is weer bijna 21 uur,
vraag 2) Lotte - ok
was ook vrij gemakkelijk, niet lotte?
vraag 6) sloeberkebebo - ok
daarna pastoor: niet ok,
daarna sloeberkebeo: nog eens ok,
daarna pastoor: ook ok.
hoe moet je rekenen?
bij vierkant 2: 3 rijen en 3 kolommen van 2 lucifers;
geeft (3.2).2 = 12 lucifers
bij vierkant 3: 4 rijen en 4 kolommen van 3 lucifers;
geeft (4.3).2 = 24 lucifers
...
vierkant 31: 32 rijen en 32 kolommen van 31 lucifers;
geeft (32.31).2 = 1984 lucifers (1)
vierkant 30: 31 rijen en 31 kolommen van 30 lucifers;
geeft (31.30).2 = 1860 lucifers (2)
verschik (1) - (2) geeft 124 lucifers
vraag 4) pastoor - ok
vraag 8 ) troontje - ok.
tot morgen met nieuwe oplossingen?
denook
vlug een evaluatie, want is weer bijna 21 uur,
vraag 2) Lotte - ok
was ook vrij gemakkelijk, niet lotte?
vraag 6) sloeberkebebo - ok
daarna pastoor: niet ok,
daarna sloeberkebeo: nog eens ok,
daarna pastoor: ook ok.
hoe moet je rekenen?
bij vierkant 2: 3 rijen en 3 kolommen van 2 lucifers;
geeft (3.2).2 = 12 lucifers
bij vierkant 3: 4 rijen en 4 kolommen van 3 lucifers;
geeft (4.3).2 = 24 lucifers
...
vierkant 31: 32 rijen en 32 kolommen van 31 lucifers;
geeft (32.31).2 = 1984 lucifers (1)
vierkant 30: 31 rijen en 31 kolommen van 30 lucifers;
geeft (31.30).2 = 1860 lucifers (2)
verschik (1) - (2) geeft 124 lucifers
vraag 4) pastoor - ok
vraag 8 ) troontje - ok.
tot morgen met nieuwe oplossingen?
denook
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
Goeie avond denook en allen
7) Ik kom Bart tegen, van wie ik weet dat hij twee kindjes heeft; een ervan is bij hem. “Dit is mijn zoon Lucas”, zegt Bart. Als je dat weet, hoe groot is dan de kans dat ook zijn tweede kind een jongen is? ( we nemen aan dat bij de geboorte de kans op een jongen en een meisje even groot is ).
- dit probleempje is meer dan 200 jaar oud en zorgde heel lang voor discussie –
Met 2 kinders zijn er 4 mogelijkheden
Bart heeft al een jongen
1 kans valt dan ook weg
aantal kansen op een 2de jongen
1 op 3 of 33.3333%
7) Ik kom Bart tegen, van wie ik weet dat hij twee kindjes heeft; een ervan is bij hem. “Dit is mijn zoon Lucas”, zegt Bart. Als je dat weet, hoe groot is dan de kans dat ook zijn tweede kind een jongen is? ( we nemen aan dat bij de geboorte de kans op een jongen en een meisje even groot is ).
- dit probleempje is meer dan 200 jaar oud en zorgde heel lang voor discussie –
Met 2 kinders zijn er 4 mogelijkheden
Bart heeft al een jongen
1 kans valt dan ook weg
aantal kansen op een 2de jongen
1 op 3 of 33.3333%
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goeden avond allemaal
Vraag 3

Groetjes
Sloeber
Vraag 3

Groetjes
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Goede avond Denook en allemaal.
vraag 10 ABCD is een willekeurige vierhoek, zoals op onderstaande figuur. Op CD leg je willekeurig een punt P. Teken AP en een evenwijdige door D aan AP. Teken ook BP en een evenwijdige door C aan BP. De twee evenwijdigen snijden elkaar in S. Toon aan dat de oppervlakte van driehoek ABS gelijk is aan de oppervlakte van ABCD.
Stel opp = oppervlakte.
De vierhoek APSD is een trapezium waarvan de rechten AS en DP zich snijden in punt X.
Dan geldt: opp APD = opp APS (zelfde basis en zelfde hoogte).
En ook: opp APD = opp APX + opp AXD = opp APS = opp APX + opp PSX.
Dus opp AXD = opp PSX en ook opp APX = opp XSD.
Of opp AXD +APX = PSX + XSD
Of opp APD = opp DSP.
Analoog is opp PBC = opp CSP.
Samengevat: de opp van driehoek ABS = de oppervlakte van vierhoek ABCD.
vraag 10 ABCD is een willekeurige vierhoek, zoals op onderstaande figuur. Op CD leg je willekeurig een punt P. Teken AP en een evenwijdige door D aan AP. Teken ook BP en een evenwijdige door C aan BP. De twee evenwijdigen snijden elkaar in S. Toon aan dat de oppervlakte van driehoek ABS gelijk is aan de oppervlakte van ABCD.
Stel opp = oppervlakte.
De vierhoek APSD is een trapezium waarvan de rechten AS en DP zich snijden in punt X.
Dan geldt: opp APD = opp APS (zelfde basis en zelfde hoogte).
En ook: opp APD = opp APX + opp AXD = opp APS = opp APX + opp PSX.
Dus opp AXD = opp PSX en ook opp APX = opp XSD.
Of opp AXD +APX = PSX + XSD
Of opp APD = opp DSP.
Analoog is opp PBC = opp CSP.
Samengevat: de opp van driehoek ABS = de oppervlakte van vierhoek ABCD.
Sudoku, wijntjes proeven, genieten.
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Vraag 3 via Pythagoras.
Driehoek rechts, (pythagoras) 12² = (10-X)² + H² (1).
Driehoek links, (Pythagoras) 10² = X² + H² (2).
** Elimineer H in vergelijking (1) via vergelijking (2).
Of 12² = (10-X)² + 10² - X² = (10-X)² + (10-X)(10+X) =
(10-X)(10 – X +10+X) = (10-X).20 of 144 = 200 -20X
of X = (200 – 144)/20 = 2,8.
** Vergelijking (2) H² = 10² - X² = 100 – 7,84 = 92,16.
Of H = √92,16 = 9,6
Antwoord: H = 9,6
Driehoek rechts, (pythagoras) 12² = (10-X)² + H² (1).
Driehoek links, (Pythagoras) 10² = X² + H² (2).
** Elimineer H in vergelijking (1) via vergelijking (2).
Of 12² = (10-X)² + 10² - X² = (10-X)² + (10-X)(10+X) =
(10-X)(10 – X +10+X) = (10-X).20 of 144 = 200 -20X
of X = (200 – 144)/20 = 2,8.
** Vergelijking (2) H² = 10² - X² = 100 – 7,84 = 92,16.
Of H = √92,16 = 9,6
Antwoord: H = 9,6
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste Pastoor
't Is just !

Groetjes
Sloeber
't Is just !

Groetjes
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Sloeber,
Voor u is dat gemakkelijk, ge maakt die tekening, en drukt op een knopke en de computer geeft het resultaat.
Aan deze kant is dat anders. Een halve eeuw terug was er een boek genoemd "Leerboek van de Meetkunde" geschreven door Théophile GOS, iemand van Diepenbeek. Maar met dat boek leert men niet meten, wel rekenen.
Dr. Théophile Gos overleed tijdens de 2e wereldoorlog, maar zijn boeken zijn nog decennia lang gebruikt in de scholen. Heden sedert 2008 is er een standbeeld van Gos in Diepenbeek met natuurlijk de meetkundige stelling van Pythagoras erop.
Ik ben er quasi zeker van dat Meester Denook destijds ook dat boek van Gos heeft mogen doornemen.
Groeten.
Voor u is dat gemakkelijk, ge maakt die tekening, en drukt op een knopke en de computer geeft het resultaat.
Aan deze kant is dat anders. Een halve eeuw terug was er een boek genoemd "Leerboek van de Meetkunde" geschreven door Théophile GOS, iemand van Diepenbeek. Maar met dat boek leert men niet meten, wel rekenen.
Dr. Théophile Gos overleed tijdens de 2e wereldoorlog, maar zijn boeken zijn nog decennia lang gebruikt in de scholen. Heden sedert 2008 is er een standbeeld van Gos in Diepenbeek met natuurlijk de meetkundige stelling van Pythagoras erop.
Ik ben er quasi zeker van dat Meester Denook destijds ook dat boek van Gos heeft mogen doornemen.
Groeten.
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste Pastoor ,
Inderdaad U bent een CRACK in formules en al de rest ! Alles berekenen !
Amaai , dat is zeker niet mijn ding ...........tekenen dat is mijn ding .
Maar hebt U al eens een cursus en/of handleiding van een goed tekenprogramma ( Pro Engineering ; Autocad ; Anvil 5000 ; Inventor enz enz ) bekeken en/of aangeleerd ? En dan alles in practijk toepassen op een computer ? Maar inderdaad eenmaal de tekening is aangemaakt is er heeeeeel veeeeeeeel informatie beschikbaar . ' t Is tenslotte een grote rekenmachine .
Best dat niet iedereen hetzelfde geschoold is , want er zijn altijd meerdere oplossingen voor eenzelfde probleem . Dat maakt het zo boeiend dat wij de oplossingen van elkaar kunnen vergelijken . Of niet soms ??
Groetjes
Sloeber
PS Er komen geregeld nieuwe versies van het teken pakket uit ......dus telken male opnieuw alles aanleren en leren toepassen ......gemakkelijk is toch anders .......
Inderdaad U bent een CRACK in formules en al de rest ! Alles berekenen !
Amaai , dat is zeker niet mijn ding ...........tekenen dat is mijn ding .
Maar hebt U al eens een cursus en/of handleiding van een goed tekenprogramma ( Pro Engineering ; Autocad ; Anvil 5000 ; Inventor enz enz ) bekeken en/of aangeleerd ? En dan alles in practijk toepassen op een computer ? Maar inderdaad eenmaal de tekening is aangemaakt is er heeeeeel veeeeeeeel informatie beschikbaar . ' t Is tenslotte een grote rekenmachine .
Best dat niet iedereen hetzelfde geschoold is , want er zijn altijd meerdere oplossingen voor eenzelfde probleem . Dat maakt het zo boeiend dat wij de oplossingen van elkaar kunnen vergelijken . Of niet soms ??
Groetjes
Sloeber
PS Er komen geregeld nieuwe versies van het teken pakket uit ......dus telken male opnieuw alles aanleren en leren toepassen ......gemakkelijk is toch anders .......
Laatst gewijzigd door sloeberkebebo op 26 nov 2009, 18:47, 2 keer totaal gewijzigd.
Meten is weten - Carpe diem
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Voorbeeld van een eenvoudig 2D tekeningske ........Vele malen verkleind !




Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste leerlingen,
na wat heen en weer gediscuteer hier, evalueren we verder.
vraag 7) lotte - mooi ok
de mogelijkheden met twee kinderen zijn: MM, MJ, JM, JJ.
Vermits er al een jongen is valt MM weg.
Blijven over: MJ, JM en JJ,
en dus 1 kans op 3 dat er nog een jongen is.
Vroeger redeneerde men zo: er is altijd één kans op twee voor een
jongen; dus was het antwoord hier 1 op 2.
Later zag men in dat dit verkeerd was.
Er is hier sprake van een 'voorwaardelijke' kans.
Die luit als volgt:
wat is de kans op een jongen, ALS (=OP VOORWAARDE DAT) er
al een jongen is.
vraag 3) sloeberkebebo - ok
later pastoor, ook ok.
Sloeberkebebo rekende met cosinusregel,
pastoor werkte met Pythagoras.
Het kon nog wat korter, ook met Pythagoras, omdat de driehoek gelijk-
benig was (-twee gelijke zijden-).
Zie hierna
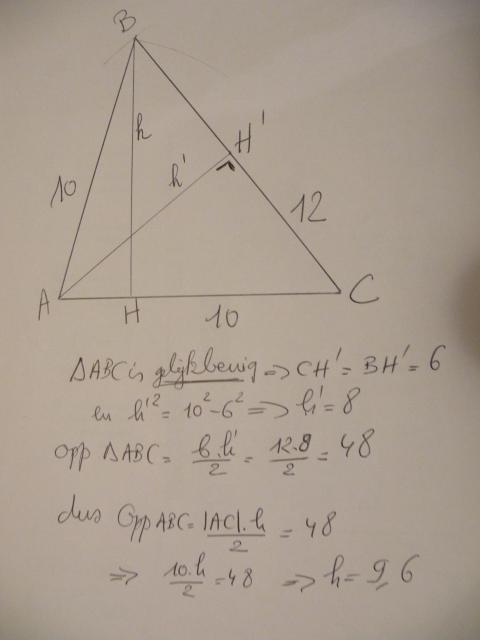
10) pastoor - ok,
doch onjuiste besluiten ook, die wel van geen nut waren voor het bewijs.
Je stelt o.a. dat driehoeken APD en DPS dezelfde opp hebben.
Dat is niet zo, maar, dit was niet nodig voor het bewijs, zoals ik zei.
Sloeberkebo, je maakte een mooie tekening en schreef er bij dat de
driehoeken even groot zijn, maar een bewijs gaf je niet.
Hierna nog eens de figuur met een kortere uitleg.
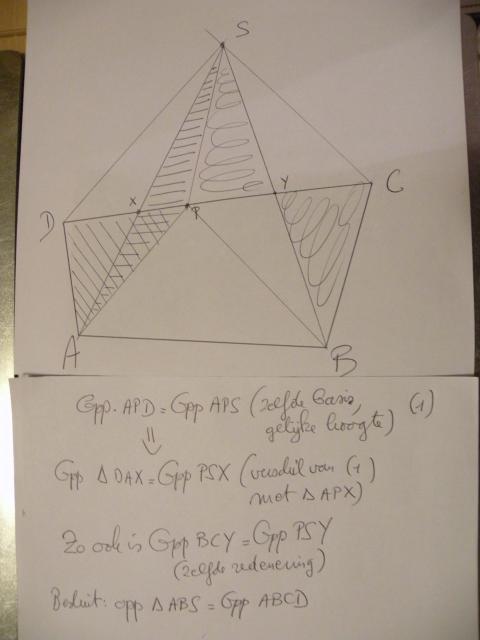
Dit was het weer; blijven over, vragen 1, 5 en het model uit vraag 9.
Tot morgen?
denook
na wat heen en weer gediscuteer hier, evalueren we verder.
vraag 7) lotte - mooi ok
de mogelijkheden met twee kinderen zijn: MM, MJ, JM, JJ.
Vermits er al een jongen is valt MM weg.
Blijven over: MJ, JM en JJ,
en dus 1 kans op 3 dat er nog een jongen is.
Vroeger redeneerde men zo: er is altijd één kans op twee voor een
jongen; dus was het antwoord hier 1 op 2.
Later zag men in dat dit verkeerd was.
Er is hier sprake van een 'voorwaardelijke' kans.
Die luit als volgt:
wat is de kans op een jongen, ALS (=OP VOORWAARDE DAT) er
al een jongen is.
vraag 3) sloeberkebebo - ok
later pastoor, ook ok.
Sloeberkebebo rekende met cosinusregel,
pastoor werkte met Pythagoras.
Het kon nog wat korter, ook met Pythagoras, omdat de driehoek gelijk-
benig was (-twee gelijke zijden-).
Zie hierna

10) pastoor - ok,
doch onjuiste besluiten ook, die wel van geen nut waren voor het bewijs.
Je stelt o.a. dat driehoeken APD en DPS dezelfde opp hebben.
Dat is niet zo, maar, dit was niet nodig voor het bewijs, zoals ik zei.
Sloeberkebo, je maakte een mooie tekening en schreef er bij dat de
driehoeken even groot zijn, maar een bewijs gaf je niet.
Hierna nog eens de figuur met een kortere uitleg.

Dit was het weer; blijven over, vragen 1, 5 en het model uit vraag 9.
Tot morgen?
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
vraag 9

groetjes
Sloeber

groetjes
Sloeber
Meten is weten - Carpe diem