Wiskundige problemen en probleempjes 2
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Meester Denook en Pastoor ,
Ik heb het ook eens geprobeerd !
Hier mijn resultaat :

Sloeber
Ik heb het ook eens geprobeerd !
Hier mijn resultaat :

Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Lotte,
Ontbinding in factoren: als C juist berekend is, dan is D dat ook.
C = √50 + √2 = √(5.5.2) + √2 = 5√2 + √2 = 6√2
D = √98 - √2 = √(2.7.7) - √2 = 7√2 - √2 = 6√2
Een rekenmachientje kan dat niet omdat het aantal cijfers na de komma oneindig is. Zelf de grootste computer kan dat niet om dezelfde reden.
Voor zulke zaken worden de computer programma's anders geschreven.
Iedereen krijgt eenmaal per jaar de eindafrekening van het elektriciteits verbruik. Probeer maar eens met een rekenmachientje lijn per lijn na te rekenen, er zijn berekeningen die niet kloppen met de cijfers na de komma en er zijn verkeerde afrondingen. Het is met een PC berekend.
Ontbinding in factoren: als C juist berekend is, dan is D dat ook.
C = √50 + √2 = √(5.5.2) + √2 = 5√2 + √2 = 6√2
D = √98 - √2 = √(2.7.7) - √2 = 7√2 - √2 = 6√2
Een rekenmachientje kan dat niet omdat het aantal cijfers na de komma oneindig is. Zelf de grootste computer kan dat niet om dezelfde reden.
Voor zulke zaken worden de computer programma's anders geschreven.
Iedereen krijgt eenmaal per jaar de eindafrekening van het elektriciteits verbruik. Probeer maar eens met een rekenmachientje lijn per lijn na te rekenen, er zijn berekeningen die niet kloppen met de cijfers na de komma en er zijn verkeerde afrondingen. Het is met een PC berekend.
Sudoku, wijntjes proeven, genieten.
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Vraag 2: Ik leg willekeurig 3 punten op een boloppervlak. Hoe groot is de kans dat ze alle drie op eenzelfde halve bol liggen?
Als er drie punten op een boloppervlak liggen en men snijdt die bol in twee halve bollen, dan is er altijd een halve bol waarop 2 punten liggen. De kans daarvoor is 1.
De kans dat het derde punt ook op dezelfde halve bol met de twee punten
is 1/2.
Antwoord: de kans dat de 3 punten op dezelfde halve bol liggen is 1/2.
Als er drie punten op een boloppervlak liggen en men snijdt die bol in twee halve bollen, dan is er altijd een halve bol waarop 2 punten liggen. De kans daarvoor is 1.
De kans dat het derde punt ook op dezelfde halve bol met de twee punten
is 1/2.
Antwoord: de kans dat de 3 punten op dezelfde halve bol liggen is 1/2.
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond beste leerlingen en sympathisanten ,
we gaan afronden.
Sorry, doch niet vragen 2 en 9 bleven over, doch 2 en 10.
Goed gezien lotte.
vraag 10 - Lotte - OK
en dan was er vraag 2 - een bijtertje.
Pastoor redeneerde bijna juist, doch bijna is niet genoeg in de wiskunde.
Ik heb wat tijd en wil me eens laten gaan - volg maar mee ...
De vraag was: als ik willekeurig drie punten op een boloppervlak kies,
hoe groot is dan de kans dat ze alle drie op éénzelfde halve bol liggen?
Voorbereiding:
door twee verschillende punten in de ruimte gaat steeds één rechte en
een rechte weten we, loopt oneindig ver door.
voorbeeld:
neem het uiterste puntje van het piemeltje van Manneke Pis in Brussel
(P) en het middelpunt van het sleutelgat van de grote deur van het Wiite
Huis in Amerika (M), dan is er één rechte die door P en M gaat
iedere rechte door het middelpunt van een cirkel, snijdt deze cirkel vol-
gens een koorde die altijd een middellijn is van de cirkel
door drie punten niet op één rechte gelegen, gaat steeds één (plat) vlak
en een vlak loopt ook oneindig ver door in alle richtingen
voorbeeld, we nemen onze punten P en M van daarnet en als derde punt
nemen we het hoogste punt van de hoogste berg op aarde (B) - welnu
er is één vlak dat door deze drie punten P, M en B zal gaan
ieder vlak door het middelpunt van een bol, snijdt deze bol volgens een
cirkel, de grootst mogelijke cirkel, een cirkel die de bol in twee halve
bollen verdeelt
en nu ons probleem ...
-
we nemen twee van de drie willekeurige punten op de bol -
deze twee punten, samen met het middelpunt van de bol, bepalen één
vlak - dat vlak verdeelt de bol in twee halve bollen -
nu zal het derde punt op een van de halve bollen liggen en dus samen
met de eerste twee punten altijd op eenzelfde halve bol liggen -
Besluit er is steeds een halve bol te vinden waarop de drie 'willekeurig'
gekozen punten liggen, of de kans is ... 1!!!
maandag verbetering oefeningen vorige les,
en dinsdag ... geen nieuwe les,
doch enkele droedels (-zoals beloofd-) rond het getal 'pi'.
Dat heeft dan voor één keer niets met wiskunde te maken.
Bedoeling is dan ook om enkele nieuwe gezichten te leren kennen.
tot maandag en dinsdag,
denook
we gaan afronden.
Sorry, doch niet vragen 2 en 9 bleven over, doch 2 en 10.
Goed gezien lotte.
vraag 10 - Lotte - OK
en dan was er vraag 2 - een bijtertje.
Pastoor redeneerde bijna juist, doch bijna is niet genoeg in de wiskunde.
Ik heb wat tijd en wil me eens laten gaan - volg maar mee ...
De vraag was: als ik willekeurig drie punten op een boloppervlak kies,
hoe groot is dan de kans dat ze alle drie op éénzelfde halve bol liggen?
Voorbereiding:
door twee verschillende punten in de ruimte gaat steeds één rechte en
een rechte weten we, loopt oneindig ver door.
voorbeeld:
neem het uiterste puntje van het piemeltje van Manneke Pis in Brussel
(P) en het middelpunt van het sleutelgat van de grote deur van het Wiite
Huis in Amerika (M), dan is er één rechte die door P en M gaat
iedere rechte door het middelpunt van een cirkel, snijdt deze cirkel vol-
gens een koorde die altijd een middellijn is van de cirkel
door drie punten niet op één rechte gelegen, gaat steeds één (plat) vlak
en een vlak loopt ook oneindig ver door in alle richtingen
voorbeeld, we nemen onze punten P en M van daarnet en als derde punt
nemen we het hoogste punt van de hoogste berg op aarde (B) - welnu
er is één vlak dat door deze drie punten P, M en B zal gaan
ieder vlak door het middelpunt van een bol, snijdt deze bol volgens een
cirkel, de grootst mogelijke cirkel, een cirkel die de bol in twee halve
bollen verdeelt
en nu ons probleem ...
-
we nemen twee van de drie willekeurige punten op de bol -
deze twee punten, samen met het middelpunt van de bol, bepalen één
vlak - dat vlak verdeelt de bol in twee halve bollen -
nu zal het derde punt op een van de halve bollen liggen en dus samen
met de eerste twee punten altijd op eenzelfde halve bol liggen -
Besluit er is steeds een halve bol te vinden waarop de drie 'willekeurig'
gekozen punten liggen, of de kans is ... 1!!!
maandag verbetering oefeningen vorige les,
en dinsdag ... geen nieuwe les,
doch enkele droedels (-zoals beloofd-) rond het getal 'pi'.
Dat heeft dan voor één keer niets met wiskunde te maken.
Bedoeling is dan ook om enkele nieuwe gezichten te leren kennen.
tot maandag en dinsdag,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
verbetering oefeningen ONTBINDEN IN FACTOREN van 4 januari
1) 4x² + (4/3)x + 1/9 = (2a + 1/3)²
2) 18a - 2ax² = 2a.(9 - x²) = 2a.(3 + x).(3 - x)
3) 125 - x-tot zesde macht = 5³ - (x²)³
= (5 - x²).(5² + 5x² + (x²)²)= (5-x²).(25 + 5x² + x-tot vierde macht)
4) 9a²b² - 3ab + 1/4 = (3ab - 1/2)²
5) 144x² - 81y² = (12x + 9y).(12x - 9y)
6) 8p³ + 27q³ = (2p)³ + (3q)³ = (2p + 3q).((2p)² + (2p).(3q) + (3q)²)
= (2p + 3q).(4p² + 6pq + 9q²)
dit was het -
morgen zoals al aangekondigd, geen nieuwe les,
doch ENKELE DROEDELS ROND HET GETAL PI.
Dit is dan voor IEDEREEN ... ook de niet-wiskundige-lezers hier,
ben benieuwd,
tot morgen,
denook
verbetering oefeningen ONTBINDEN IN FACTOREN van 4 januari
1) 4x² + (4/3)x + 1/9 = (2a + 1/3)²
2) 18a - 2ax² = 2a.(9 - x²) = 2a.(3 + x).(3 - x)
3) 125 - x-tot zesde macht = 5³ - (x²)³
= (5 - x²).(5² + 5x² + (x²)²)= (5-x²).(25 + 5x² + x-tot vierde macht)
4) 9a²b² - 3ab + 1/4 = (3ab - 1/2)²
5) 144x² - 81y² = (12x + 9y).(12x - 9y)
6) 8p³ + 27q³ = (2p)³ + (3q)³ = (2p + 3q).((2p)² + (2p).(3q) + (3q)²)
= (2p + 3q).(4p² + 6pq + 9q²)
dit was het -
morgen zoals al aangekondigd, geen nieuwe les,
doch ENKELE DROEDELS ROND HET GETAL PI.
Dit is dan voor IEDEREEN ... ook de niet-wiskundige-lezers hier,
ben benieuwd,
tot morgen,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond beste leerlingen,
en, NU VOORAL, ook aan de andere lezers hier.
Vanavond geen wiskunde-les,
noch wiskundeproblemen.
Neen, zoals reeds aangekondigd: enkele DROEDELS rond pi.
Heeft nu eens niks met wiskunde te maken -
enkel wat nadenken, glimlachen en 'ha-ha, ik heb het'...
Om de spanning er wat in te houden en iedereen die later komt
lezen ook een kans te geven ANTWOORDEN we NIET OP DE TOPIC.
Ik krijg al eens een privéberichtje van mensen die ik ken van andere
topics, met de mededeling dat ze hier regelmatig komen lezen, doch niet
meespelen omdat het te moeilijk is, of ze te laat zijn ...
Ik weet niet in hoeverre dat allemaal waar is ... dat hier komen lezen dan.
Daarom deze droedels nu. Geen reden om te zeggen "te moeilijk".
Geen reden om te laat te zijn, want niemand post hier zijn antwoord.
Oproep aan iedereen die hier langs komt: zoek mee!!
Vanaf één gevonden antwoord mag je al doorsturen privé!!
Ben benieuwd hoeveel niet-leerlingen zich gaan melden - spannend.
Achteraf hier de antwoorden + aantal juist-opgeloste droedels.
Hier gaan we
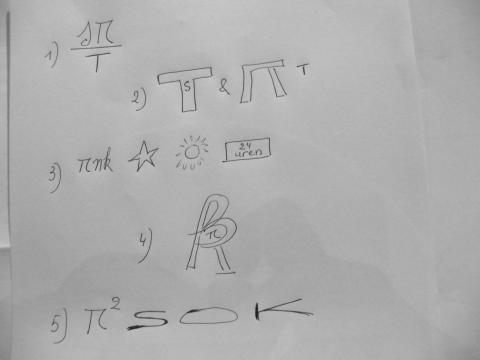
denk er aan - voor de spanning : NIET ANTWOORDEN HIER
tot over enkele dagen,
denook
en, NU VOORAL, ook aan de andere lezers hier.
Vanavond geen wiskunde-les,
noch wiskundeproblemen.
Neen, zoals reeds aangekondigd: enkele DROEDELS rond pi.
Heeft nu eens niks met wiskunde te maken -
enkel wat nadenken, glimlachen en 'ha-ha, ik heb het'...
Om de spanning er wat in te houden en iedereen die later komt
lezen ook een kans te geven ANTWOORDEN we NIET OP DE TOPIC.
Ik krijg al eens een privéberichtje van mensen die ik ken van andere
topics, met de mededeling dat ze hier regelmatig komen lezen, doch niet
meespelen omdat het te moeilijk is, of ze te laat zijn ...
Ik weet niet in hoeverre dat allemaal waar is ... dat hier komen lezen dan.
Daarom deze droedels nu. Geen reden om te zeggen "te moeilijk".
Geen reden om te laat te zijn, want niemand post hier zijn antwoord.
Oproep aan iedereen die hier langs komt: zoek mee!!
Vanaf één gevonden antwoord mag je al doorsturen privé!!
Ben benieuwd hoeveel niet-leerlingen zich gaan melden - spannend.
Achteraf hier de antwoorden + aantal juist-opgeloste droedels.
Hier gaan we
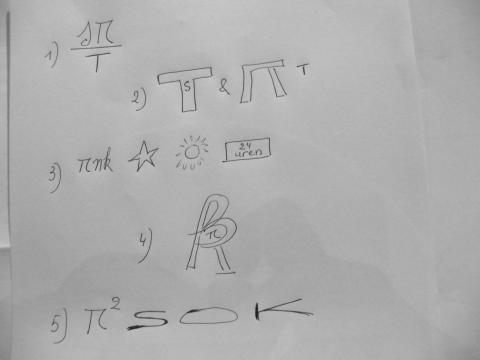
denk er aan - voor de spanning : NIET ANTWOORDEN HIER
tot over enkele dagen,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
en vooral het kleine kransje medespelers,
morgenavond om 21 uur ben ik noch thuis,
noch in de nabijheid van een pc,
daarom ...
volgende reeks wiskundige problemen en propleempjes
hier op woensdagavond 27 januari, ook om 21 uur,
groetjes,
denook
en vooral het kleine kransje medespelers,
morgenavond om 21 uur ben ik noch thuis,
noch in de nabijheid van een pc,
daarom ...
volgende reeks wiskundige problemen en propleempjes
hier op woensdagavond 27 januari, ook om 21 uur,
groetjes,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
na de succesloze droedels ...
weer onze tien klassieke wiskundeproblemen en probleempjes,
1) Het gemiddelde van 1/0,22222 ... en 1/0,66666... is gelijk aan ....??
3) A is een natuurlijk getal, gelijk aan het dubbele van de som van zijn cijfers,
B is een natuurlijk getal, gelijk aan het drievoud van de som van zijn cijfers.
Hoeveel is dan A + B ?
4) Hoeveel drietallen positieve reële getallen a, b, en c zijn er waarvoor geldt:
a.b.c = 1 én a + b + c = 1?
5) Hoeveel verschillende getallen zijn er die het product zijn van twee verschillende
getallen uit de rij (1, 2, 3, 4, 5, 6)?
6) Eén van volgende maten is het volume van een blikje cola. Welk?
A) 33 cm³, B) 330 cm³, C) 0,33 m³, D) 0,033 m³, E) 0,0033 m³
7) Een punt P ligt willekeurig op de schuine zijde van een rechthoekige driehoek ABC,
met rechte hoek in A en AB als kortste zijde.
De loodlijn uit P op AB snijdt AB in M,
De loodlijn uit P op AC snijdt AC in N.
Waar moet P liggen, zodat het lijnstuk MN zo kort mogelijk is?
A) in B,
B) in C,
C) in het voetpunt van de loodlijn uit A op BC,
D) in het snijpunt van de bissectrice uit A met BC,
E) in het midden van lijnstuk BC?
8 ) Stel D(Denook), L(Lotte), O(Oomski), P(Pastoor), S(Sloeberkebebo), T(Troontje)
en stel dat
D en S samen minder wegen dan T en O samen, en
T en P samen minder wegen dan L en S samen.
Wat is dan waar?
A) O en L wegen samen meer dan D en T samen,
B) O en P wegen samen meer dan T en L samen,
C) D en P wegen samen minder dan L en O samen,
D) D en S wegen samen minder dan T en L samen
E) D, S en T wegen samen evenveel als O, P en L samen.
9)
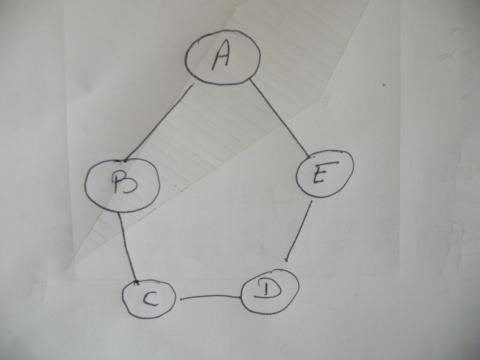
A, B, C, D en E zijn vijf natuurlijke getallen waarvoor geldt dat:
als je twee of drie naast elkaar liggende getallen optelt, is de som nooit een drievoud.
Hoeveel van deze getallen zijn dan zelf wel een drievoud?
A)geen, B) een, C) twee, D) drie, E) kan niet bepaald worden
10) Op een vergadering geeft elke aanwezige juist één keer een hand aan elke andere aanwezige.
Er zijn 36 handdrukken tussen twee dames en 28 tussen twee heren.
Hoeveel handdrukken zijn er dan tussen een heer en een dame?
Ik vind dit zelf een mooie mix ... genieten maar ...
Nieuwe spelers lezen eerst blz 1.
Tot morgen ... denook
na de succesloze droedels ...
weer onze tien klassieke wiskundeproblemen en probleempjes,
1) Het gemiddelde van 1/0,22222 ... en 1/0,66666... is gelijk aan ....??

3) A is een natuurlijk getal, gelijk aan het dubbele van de som van zijn cijfers,
B is een natuurlijk getal, gelijk aan het drievoud van de som van zijn cijfers.
Hoeveel is dan A + B ?
4) Hoeveel drietallen positieve reële getallen a, b, en c zijn er waarvoor geldt:
a.b.c = 1 én a + b + c = 1?
5) Hoeveel verschillende getallen zijn er die het product zijn van twee verschillende
getallen uit de rij (1, 2, 3, 4, 5, 6)?
6) Eén van volgende maten is het volume van een blikje cola. Welk?
A) 33 cm³, B) 330 cm³, C) 0,33 m³, D) 0,033 m³, E) 0,0033 m³
7) Een punt P ligt willekeurig op de schuine zijde van een rechthoekige driehoek ABC,
met rechte hoek in A en AB als kortste zijde.
De loodlijn uit P op AB snijdt AB in M,
De loodlijn uit P op AC snijdt AC in N.
Waar moet P liggen, zodat het lijnstuk MN zo kort mogelijk is?
A) in B,
B) in C,
C) in het voetpunt van de loodlijn uit A op BC,
D) in het snijpunt van de bissectrice uit A met BC,
E) in het midden van lijnstuk BC?
8 ) Stel D(Denook), L(Lotte), O(Oomski), P(Pastoor), S(Sloeberkebebo), T(Troontje)
en stel dat
D en S samen minder wegen dan T en O samen, en
T en P samen minder wegen dan L en S samen.
Wat is dan waar?
A) O en L wegen samen meer dan D en T samen,
B) O en P wegen samen meer dan T en L samen,
C) D en P wegen samen minder dan L en O samen,
D) D en S wegen samen minder dan T en L samen
E) D, S en T wegen samen evenveel als O, P en L samen.
9)

A, B, C, D en E zijn vijf natuurlijke getallen waarvoor geldt dat:
als je twee of drie naast elkaar liggende getallen optelt, is de som nooit een drievoud.
Hoeveel van deze getallen zijn dan zelf wel een drievoud?
A)geen, B) een, C) twee, D) drie, E) kan niet bepaald worden
10) Op een vergadering geeft elke aanwezige juist één keer een hand aan elke andere aanwezige.
Er zijn 36 handdrukken tussen twee dames en 28 tussen twee heren.
Hoeveel handdrukken zijn er dan tussen een heer en een dame?
Ik vind dit zelf een mooie mix ... genieten maar ...
Nieuwe spelers lezen eerst blz 1.
Tot morgen ... denook
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
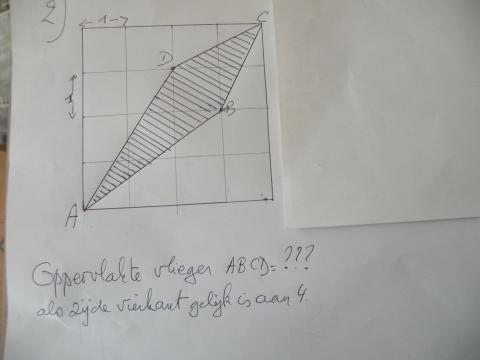
Vraag 2)
Een diagonaal van een vierkant met zijde 1 is d² = 1² + 1² of d = √2
Driehoek CDB :
basis = DB = √2, hoogte = 1,5 √2. Oppervlakte = (√2 * (1,5 √2))/2 = 1,5
Driehoek ADB :
basis = DB = √2, hoogte = 2,5 √2. Oppervlakte = (√2 * (2,5 √2))/2 = 2,5
Oppervlakte ABCD = 2,5 + 1,5 = 4.
Een diagonaal van een vierkant met zijde 1 is d² = 1² + 1² of d = √2
Driehoek CDB :
basis = DB = √2, hoogte = 1,5 √2. Oppervlakte = (√2 * (1,5 √2))/2 = 1,5
Driehoek ADB :
basis = DB = √2, hoogte = 2,5 √2. Oppervlakte = (√2 * (2,5 √2))/2 = 2,5
Oppervlakte ABCD = 2,5 + 1,5 = 4.
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goeden avond allemaal
Vraag 7
C) in het voetpunt van de loodlijn uit A op BC
Tekening volgt ..............
Groetjes
Sloeber
Vraag 7
C) in het voetpunt van de loodlijn uit A op BC
Tekening volgt ..............
Groetjes
Sloeber
Meten is weten - Carpe diem
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare

Meten is weten - Carpe diem