duplicaat
Laatst gewijzigd door pastoor op 10 feb 2010, 19:13, 3 keer totaal gewijzigd.
Sudoku, wijntjes proeven, genieten.
Wiskundige problemen en probleempjes 2
Beste denook en allen een goeie avond
vraag 6
stel getal gelijk aan x,
dan 100x = x + 297,
99x = 297,
x = 297/99 = 3
getal : 3
groetjes
lotte.
vraag 6
stel getal gelijk aan x,
dan 100x = x + 297,
99x = 297,
x = 297/99 = 3
getal : 3
groetjes
lotte.
Laatst gewijzigd door lotte op 09 feb 2010, 20:39, 1 keer totaal gewijzigd.
Goeden avond allemaal
Vraag 4)
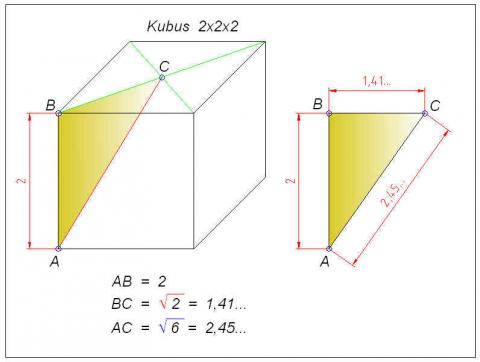
De afstand van het middelpunt van het bovenvlak tot een hoekpunt van het ondervlak van een kubus met zijde 2 is gelijk aan de vierkantswortel uit 6 ====>>>> 2,45...
Groetjes
Sloeber
Vraag 4)
De afstand van het middelpunt van het bovenvlak tot een hoekpunt van het ondervlak van een kubus met zijde 2 is gelijk aan de vierkantswortel uit 6 ====>>>> 2,45...
Groetjes
Sloeber
Meten is weten - Carpe diem
goedenavond!
Vraag 8:
Hoek E = 150°
De hoeken van ABE zijn elk 60°
ADE en BEC zijn gelijkbenige driehoeken
daarin is hoek a en b elk 30°
en dus in hoeken ADE en BEC zijn de onderhoeken elk 75°
Dus de kleine hoeken van DEC zijn elk 15°
Dus Hoek E van DEC is 150°
tekening achteraf bijgezet.
Vraag 8:
Hoek E = 150°
De hoeken van ABE zijn elk 60°
ADE en BEC zijn gelijkbenige driehoeken
daarin is hoek a en b elk 30°
en dus in hoeken ADE en BEC zijn de onderhoeken elk 75°
Dus de kleine hoeken van DEC zijn elk 15°
Dus Hoek E van DEC is 150°
tekening achteraf bijgezet.
Laatst gewijzigd door oomski op 10 feb 2010, 19:29, 3 keer totaal gewijzigd.
Wie op wraak zint, houdt zijn eigen wonden open.
goede avond allen,
10) Als A, B en C cijfers zijn , en AAA + B = BCCC, wat zijn dan A, B en C?
A=9----B=1------C=0
999+1=1000
slaapwel,
troontje
10) Als A, B en C cijfers zijn , en AAA + B = BCCC, wat zijn dan A, B en C?
A=9----B=1------C=0
999+1=1000
slaapwel,
troontje
goede avond iedereen,
en vooral ons voltallig klasje,
met een proficiat.
Inderdaad:
pastoor, lotte, sloeberkebebo, oomski en troontje,
in die volgorde,
losten ieder een oefening volledig correct op.
Blijven nog over: vragen 1, 2, 3, 5 en 7
tot morgen?
denook,
Oh ja, pastoor gaf ook nog een antwoord: "duplicaat",
na tweemaal het antwoord te hebben bewerkt.
Wie kan mij hierbij helpen... ik versta het niet ...
en vooral ons voltallig klasje,
met een proficiat.
Inderdaad:
pastoor, lotte, sloeberkebebo, oomski en troontje,
in die volgorde,
losten ieder een oefening volledig correct op.
Blijven nog over: vragen 1, 2, 3, 5 en 7
tot morgen?
denook,
Oh ja, pastoor gaf ook nog een antwoord: "duplicaat",
na tweemaal het antwoord te hebben bewerkt.
Wie kan mij hierbij helpen... ik versta het niet ...
Met de software op "mijn" PC is het niet mogelijk
iets weg te doen dat al op het seniorennet weggeschreven is.
Ik moet op zijn minst iets laten staan (van daar het woord duplicaat)..
Heel vervelend.
Lotte had terzelfdertijd met mij ook een duplicaat.
Maar zij kan het wel elimineren.
.
iets weg te doen dat al op het seniorennet weggeschreven is.
Ik moet op zijn minst iets laten staan (van daar het woord duplicaat)..
Heel vervelend.
Lotte had terzelfdertijd met mij ook een duplicaat.
Maar zij kan het wel elimineren.
.
Sudoku, wijntjes proeven, genieten.
Je kan alleen maar deleten zolang er niemand na jou heeft gepost. 
Wie op wraak zint, houdt zijn eigen wonden open.
Beste denook en allen
vraag 1
van klein naar groot:
A, D, B, E, C
weet 5-tot macht(-1) = (1/5) = 0,2
en (0,5)-tot macht(-1) = 1/(0,5) = 2
vraag 1
van klein naar groot:
A, D, B, E, C
weet 5-tot macht(-1) = (1/5) = 0,2
en (0,5)-tot macht(-1) = 1/(0,5) = 2
Goede avond allemaal.
Vraag 7) Ik schrijf alle mogelijke getallen van zes cijfers, door alleen 1 en 2 te gebruiken, (-voorbeeld: 211222-). Als ik uit die rij getallen een willekeurig getal aanduid, wat is dan de kans dat er precies driemaal een '1' in staat, en wel de drie 'enen' naast elkaar?
Hoeveel getallen?
Er zijn 6 plaatsen (p) in het getal van 6 cijfers.
Per plaats zijn er 2 (n) mogelijkheden (1 of 2).
Dit levert (n tot de macht p) of 2.2.2.2.2.2 = 64 getallen.
Voorstelling. Dit zijn de 8 eerste getallen. En hierin is er precies een oplossing met driemaal een ‘1’, en de drie “enen” naast elkaar.
222222
222221
222212
222211
222122
222121
222112
222111
Men ziet hier ook dat er maar 4 juiste oplossingen mogelijk zijn, namelijk
(222111, 221112, 211122, 111222) in die 64 getallen.
De kans is 4/64 of 1/16.
Ter bevestiging, alle 64 getallen.
Horizontale voorstelling van 8 eerste getallen: met een oplossing.
222222, 222221, 222212, 222211, 222122, 222121, 222112, 222111
Horizontale voorstelling van 8 volgende getallen: met een oplossing.
221222, 221221, 221212, 221211, 221122, 221121, 221112, 221111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
212222, 212221, 212212, 212211, 212122, 212121, 212112, 212111
Horizontale voorstelling van 8 volgende getallen: met een oplossing.
211222, 211221, 211212, 211211, 211122, 211121, 211112, 211111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
122222, 122221, 122212, 122211, 122122, 122121, 122112, 122111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
121222, 121221, 121212, 121211, 121122, 121121, 121112, 121111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
112222, 112221, 112212, 112211, 112122, 112121, 112112, 112111
Horizontale voorstelling van 8 volgende getallen: met een oplossing.
111222, 111221, 111212, 111211, 111122, 111121, 111112, 111111
Vraag 7) Ik schrijf alle mogelijke getallen van zes cijfers, door alleen 1 en 2 te gebruiken, (-voorbeeld: 211222-). Als ik uit die rij getallen een willekeurig getal aanduid, wat is dan de kans dat er precies driemaal een '1' in staat, en wel de drie 'enen' naast elkaar?
Hoeveel getallen?
Er zijn 6 plaatsen (p) in het getal van 6 cijfers.
Per plaats zijn er 2 (n) mogelijkheden (1 of 2).
Dit levert (n tot de macht p) of 2.2.2.2.2.2 = 64 getallen.
Voorstelling. Dit zijn de 8 eerste getallen. En hierin is er precies een oplossing met driemaal een ‘1’, en de drie “enen” naast elkaar.
222222
222221
222212
222211
222122
222121
222112
222111
Men ziet hier ook dat er maar 4 juiste oplossingen mogelijk zijn, namelijk
(222111, 221112, 211122, 111222) in die 64 getallen.
De kans is 4/64 of 1/16.
Ter bevestiging, alle 64 getallen.
Horizontale voorstelling van 8 eerste getallen: met een oplossing.
222222, 222221, 222212, 222211, 222122, 222121, 222112, 222111
Horizontale voorstelling van 8 volgende getallen: met een oplossing.
221222, 221221, 221212, 221211, 221122, 221121, 221112, 221111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
212222, 212221, 212212, 212211, 212122, 212121, 212112, 212111
Horizontale voorstelling van 8 volgende getallen: met een oplossing.
211222, 211221, 211212, 211211, 211122, 211121, 211112, 211111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
122222, 122221, 122212, 122211, 122122, 122121, 122112, 122111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
121222, 121221, 121212, 121211, 121122, 121121, 121112, 121111
Horizontale voorstelling van 8 volgende getallen: geen oplossing.
112222, 112221, 112212, 112211, 112122, 112121, 112112, 112111
Horizontale voorstelling van 8 volgende getallen: met een oplossing.
111222, 111221, 111212, 111211, 111122, 111121, 111112, 111111
Sudoku, wijntjes proeven, genieten.
Goeden avond allemaal
Vraag 5)
Hoek alfa is gelijk aan : 65°
Groetjes
Sloeber
PS Beste Lotte
Van klein naar groot voor vraag 1) C- E- B- A-D
Vraag 5)
Hoek alfa is gelijk aan : 65°
Groetjes
Sloeber
PS Beste Lotte
Van klein naar groot voor vraag 1) C- E- B- A-D
Meten is weten - Carpe diem
Oomski, zelfs al is er niemand na mij, het gaat niet.
Uitgetest met Bakker. Het werkt niet.
Uitgetest met Bakker. Het werkt niet.
Sudoku, wijntjes proeven, genieten.
Alleen op dat kruisje klikken...raar.
Wie op wraak zint, houdt zijn eigen wonden open.
Rechts boven bij u staat er EEN vakje en daar in staat (wijzigen, een kruis en een geel blokje). Zet daar eens de muis op zonder te klikken. Dan komt er commentaar "verwijderen". Maar dat werkt niet.
Het is uitgetest bij mij samen met Bakker, bij hem ging dat, bij mij niet.
Het is uitgetest bij mij samen met Bakker, bij hem ging dat, bij mij niet.
Sudoku, wijntjes proeven, genieten.
Rechts boven mijn post staat: "citaat" "wijzigen" "X"...en ik hoef maar gewoon op die X te klikken en dan komt er een ja/neen vraag.
Wie op wraak zint, houdt zijn eigen wonden open.