Wiskundige problemen en probleempjes 2

[oomski]

Goedenavond iedereen.

Vraag 1:

A=[5+(30+A+C)/3+(15+A+C)/3]/3
A=(15+30+A+C+15+A+C)/9
9A=60+2A+2C
A=(60+2C)/7

C=[20+(15+A+C)/3+(30+A+C)/3]/3
C=(60+15+A+C+30+A+C)9
9C=105+2A+2C
C=(105+2A)/7

A=[60+2(105+2A)/7]/7
A=(420+210+4A)/49
49A=630+4A
45A=630
A=14

C=(105+2*14)/7
C=19

B=(15+14+19)/3 = 48/3
B=16

D=(30+14+19)/3 = 63/3
D=21

[denook]

goede avond iedereen,
onze vijf leerlingen maakten allen hun oefening juist,

vraag 7) lotte - ok
een kwadraat is inderdaad óf een viervoud, óf een viervoud + 1

vraag 4) pastoor - ok
overduidelijk uitgewerkt,

vraag 9) sloeberkebebo ok, maar ...
er was sprake van een 'willekeurige' rechthoek -
we moesten zelfs geen afmetingen kennen.
I en II zijn driehoeken met dezelfde hoogte
en een tweevoud van de basis I in II,
dus II / I = 2

I en III zijn gelijkvormige driehoeken (hoeken twee aan twee gelijk)
en afmetingen vermenigvuldigd met twee, dus oppervlakten maal 2² = 4,
dus III / I = 4

als opp. I, één is, dan is dus opp. II, 2 en opp. III, 4

II + III = 2 + 4 = helft rechthoek,
nu is I + IV ook helft rechthoek, met I = 1; dus IV = 5
en IV / I = 5

je oppervlakten zijn natuurlijk juist sloeberkebebo

vraag 1) oomski - ok
midden in de nacht ...
geef oomski maar vergelijkingen en ze geraakt er wel.

tot morgen voor de vijf overige problemen?

groetjes, denook

[pastoor]

Goede avond Denook.

vraag 6) Als x².(y + z²) = 40, en x, y en z zijn natuurlijke getallen, welke waarden kunnen x, y en z dan aannemen?
(y + z²) = 40/x²

Met x = 1 wordt dat (y + z² ) = 40
(x, y, z) = (1, 39 ,1), (1, 36, 2), (1, 31, 3), (1, 24, 4), (1, 15, 5) (1, 4, 6)
Met x = 2 wordt dat (y + z²) = 10
(x, y, z) = (2, 1, 3), (2, 6, 2), (2, 9, 1)

Er zijn 6 oplossingen voor X = 1 en 3 oplossingen voor X = 2.
(x, y, z) = (1, 39 ,1), (1, 36, 2), (1, 31, 3), (1, 24, 4), (1, 15, 5), (1, 4, 6),
(x, y, z) = (2, 1, 3), (2, 6, 2), (2, 9, 1)

[troontje]

goede avond allen,

vraag2Ik heb tien muntstukken met aan de ene kant een cijfer, aan de andere kant een letter.
Ik heb ook vier dobbelstenen. Ik gooi de tien muntstukken en de vier dobbelstenen.
Bij de muntstukken wil ik alleen cijfers gooien; bij de dobbelstenen alleen 'enen'.
Welke kans is de grootste?


munten 10/20 =1/2 (de grootste kans)
4 dobbelstenen 4/24=1/6


troontje

[lotte]

denook

Vraag 8

Antw : 35 dagen
man drinkt per dag 1/14 van het vat
dronk na 10 dagen 10/14
vat is leeg, vrouw dronk dus
4/14 op 10 dagen
1/14 op 10/4
na 14 dagen = 10/4*14

[pastoor]

Troontje, andere cijfers met hetzelfde besluit.

Munt: c =cijfer, l = letter.
Werpen van 1 munt is er (c,l), kans ‘1 cijfer’ = 1/2.
Werpen van 2 munten is er (cc, cl, lc, ll), kans ‘2 cijfers’ = (1/2)(1/2)= 1/4
……….
Werpen van 10 munten,
kans ‘10 cijfers’ = (1/2)(1/2)…(1/2)= 1/1024.

Dobbelsteen:
Werpen van 1 dobbelsteen is er (1, 2, 3, ..6), kans een ‘een’ = 1/6.
Werpen van 2 dobbelstenen is er (1,1)(1,2)(1,3)……(6,6), kans twee ‘enen’ = (1/6)(1/6) = 1/36.
Werpen van 4 dobbelstenen,
kans vier ‘enen’ = (1/6)(1/6)(1/6)(1/6)= 1/1296.


Antwoord: De kans is het grootste bij de munten.

[troontje]

Pastoor,ik kan dit niet zo uitwerken zoals jij dat kunt en doet maar 'k wist wel dat het iets te maken had met 1/2 en 1/6 ,maar dat zal zeker niet voldoende zijn voor de meester

slaapwel allen,

troontje

[oomski]

Voor vraag 8 van Thomas van der Noot, kwam ik ook op 35 dagen zoals Lotte.

[sloeberkebebo]

Dag allemaal ,

Voor vraag 8 komt het op geen tonneke zulle !



Schol

Sloeber

[denook]

goede avond,
we gaan verder...

vraag 6) pastoor - ok,

vraag 8 lotte - ok,
bevestigd door oomski

vraag 2) pastoor - ok,
na mislukte poging door troontje
(- versta je het nu troontje -
is wel klaar uitgelegd door pastoor-)

blijven over: vragen 3 en 5

een hint voor 5:
in iedere driehoek is elke zijde
- langer dan het verschil van de twee ander zijden,
- korter dan de som van de twee andere zijden.

tot morgen?
denook

oh ja, sloeberkebebo,
bedankt voor de traktatie ...

[pastoor]

Goede avond Denook,

Vraag 5) Als t, t + 1 en t + 2 lengten zijn van de zijden van een driehoek, dan moet t voldoen aan: A) t > 1, B) t < 1, C) t is verschillende van 2, D) t < 3, E) t = 3.

In een driehoek is de lengte van elke zijde kleiner dan de som van de lengten van de twee andere zijden.
2t + 3 > t, of t > -3.
2t + 2 > t + 1, of t > -1.
2t + 1 > t + 2 of t > 1, de meest stringente beperking.
Antwoord: A) t > 1.

* * * * * * * * * *

Wat nu volgt heeft Meester Denook voorgesteld, ik geloof dat niet.
In een driehoek is de lengte van elke zijde langer dan het verschil van de twee ander zijden.
t > t + 2 - t - 1 of t >1.
t + 1 > t + 2 – t, of t > 1.
t + 2 > t + 1 – t, of t > -1.

[lotte]

meester denook,

vraag 3
a² + a - b² - b
a² - b² + a - b
(a² - b²) + (a - b)
(a + b).(a - b) + (a - b)
(a - b).((a + b) + 1)
(a - b).(a + b + 1)
(a + b + 1) is een factor
antwoord D

goeie avond en groetjes allen
lotte.

[denook]

goede avond iedereen,

er bleven twee problemen gisteren -
ze zijn vandaag van de baan -
mooi pastoor en lotte,
en met voldoende uitleg.

Zo kunnen we op vrijdagavond deze reeks afsluiten.

Nieuwe afspraak, bij leven en welzijn,
dinsdag 9 maart aanstaande,

tot dan,
denook

[denook]

goede avond iedereen,
en vooral de leerlingen van ons sympathiek klasje

hier weer tien 'wiskundige problemen en probleempjes'

1) Een wijnhandelaar heeft een vat wijn van 228 liter dat hem 4560 Fr
kost en een tweede vat van 450 liter dat hem 11700 Fr kost.
Hij wil nu 450 liter mengen die hem 24 Fr per liter kosten.
Hoeveel neemt hij daarvoor van elke soort?
(- sorry voor de Fr in plaats ven de Euro-)

2) Als bij drie opeenvolgende natuurlijke getallen, het kwadraat van het
middelste getal, één meer is dan het product van de andere twee, wat
zijn dan de drie getallen?

3) Ik heb een zinken plaat van 28 cm bij 21 cm.
Ik kan ze op twee manieren tot een cilinder lassen: eenmaal met 21 cm
als hoogte en eenmaal met 28 cm als hoogte.
Wat is het verschil tussen de inhouden van beide cilinders?
(- we nemen aan dat ze ook elk een bodem krijgen -)

4) Een Arabische puzzel van bij de start van de algebra, lang geleden.
Drie vrienden slapen naast een doos dadels.
De eerste wordt wakker en eet 1/3 van de dadels - valt weer in slaap,
de tweede wordt wakker en eet 1/3 van de overige dadels - slaapt weer,
de derde wordt wakker en eet 1/3 van de resterende dadels - slaapt in.
's Morgens liggen er nog acht dadels.
Hoeveel lagen er de avond voordien?

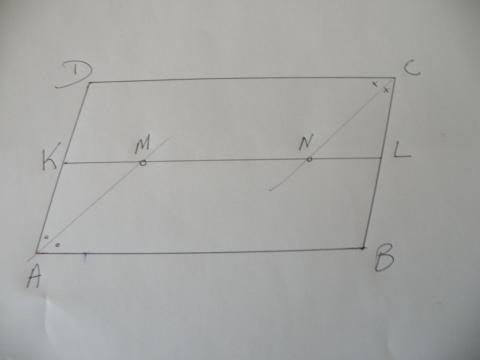
5) ABCD is een parallellogram.
K is midden van AD en L is midden van BC.
De bissectrice in A snijdt KL in M,
de bissectrice in C snijdt KL in N.
Bestaat er een verband tussen de afstanden AB, AD en MN?




6) Drie mannen gooien elk één dobbelsteen. Welke kans is grootst?
- niemand gooit een zes, of
- iedereen gooit een verschillend getal.

7) In een kubus met ribbe 1 past mooi een bol.
In de bol past weer mooi een kleinere kubus.
Wat is de inhoud van deze laatste kubus?
(vergast sloeberkebebo ons met een mooie figuur?)

8 ) We stellen de TIEN cijfers ( 0, 1, ..., 8, 9) in willekeurige volgorde
voor door de letters A, B, C, ..., H, I, J.
Als volgende som ABC + DEF = GHIJ,
wat zijn dan de cijfers A, B, C, ... , H, I, J?

9 ) Een leraar geeft volgend strafwerk aan een leerling:
uit een boek moet hij overschrijven -
1 woord uit hoofdstuk één,
2 woorden uit hoofdstuk twee,
3 woorden uit hoofdstuk drie,
...
Na veertien hoofdstukken heeft hij de helft van alle woorden geschreven.
Hoeveel hoofdstukken telt het boek?

10 ) Als 7a - 12 = 2a + k = 3a + 8,
dan is k = ???

succes iedereen, en ...
... nog eens ... nieuwe leerlingen graag welkom -
ze lezen wel eerst blz 1

tot morgen,
denook

[lotte]

Avond denook

vraag 3
antwoord: is altijd zo,
voorbeeld 4,5 en 6 geeft 5² = 4*6 + 1
5,6 en 7 geeft 6² = 5*7 + 1
6,7 en 8 geeft 7² = 6*8 + 1
enz.