Wiskundige problemen en probleempjes 2
-
troontje - Lid geworden op: 14 dec 2004, 10:03
goeie avond,
ik probeer sloeberkebebo,
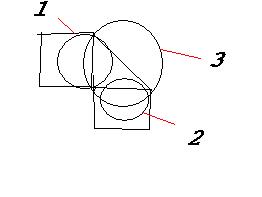de verhoudingen kloppen wel niet in mijn tekening met paint is het moeilijk
1ste cirkel,3.14x40x40=5024
2de cirkel ,3.14x30x30=2826
3de cirkel,3.14X50X50=7850
1ste en 2 de cirkel is samen 7850- 3925(halve cirkel 3)=3925?????? oppervlakte van de twee maantjes
troontje
ik probeer sloeberkebebo,
de verhoudingen kloppen wel niet in mijn tekening met paint is het moeilijk1ste cirkel,3.14x40x40=5024
2de cirkel ,3.14x30x30=2826
3de cirkel,3.14X50X50=7850
1ste en 2 de cirkel is samen 7850- 3925(halve cirkel 3)=3925?????? oppervlakte van de twee maantjes
troontje
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
Troontje en sloeberke,
ik was er ook mee bezig, ben zeker ook niet zeker, en vraag me geen tekening
opp. halve cirkel blauw maantje 0.5*3.14*40² = 2512+
opp. halve cirkel groen maantje 0.5*3.14*30² = 1413+
opp. rechthoekige driehoek 0.5*60*80 = 2400 -
opp. grote halve cirkel 0.5*3.14*50² = 3925
opp. van de 2 kleine cirkels samen = 2400
groetjes en mooie vakantie dagen aan allen
lotte.
ik was er ook mee bezig, ben zeker ook niet zeker, en vraag me geen tekening
opp. halve cirkel blauw maantje 0.5*3.14*40² = 2512+
opp. halve cirkel groen maantje 0.5*3.14*30² = 1413+
opp. rechthoekige driehoek 0.5*60*80 = 2400 -
opp. grote halve cirkel 0.5*3.14*50² = 3925
opp. van de 2 kleine cirkels samen = 2400
groetjes en mooie vakantie dagen aan allen
lotte.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Hier dan de oplossing voor de maantjes
Vele groetjes
Sloeberkebebo
Hoe berekenen :
opp. halve cirkel R40===> 0.5*pi*40² ===> 2513,27
opp. halve cirkel R30===> 0.5*pi*30² ===> 1413,72
Samen = 3926,99 (1)
opp. halve cirkel R50===> 0.5*pi*50² ===> 3926,99
opp. rechthoekige driehoek===> 0.5*60*80 = 2400
Verschil = 1526,99 (2)
opp. van de 2 maantjes samen = (1)-(2) = 2400
Vele groetjes
Sloeberkebebo
Hoe berekenen :
opp. halve cirkel R40===> 0.5*pi*40² ===> 2513,27
opp. halve cirkel R30===> 0.5*pi*30² ===> 1413,72
Samen = 3926,99 (1)
opp. halve cirkel R50===> 0.5*pi*50² ===> 3926,99
opp. rechthoekige driehoek===> 0.5*60*80 = 2400
Verschil = 1526,99 (2)
opp. van de 2 maantjes samen = (1)-(2) = 2400
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
mooi gedaan sloeberkebebo,
maar ...
kan er geen kleine proficiat af voor lotte,
jouw sympathieke medeleerlinge
en haar juist antwoord,
en ... een schouderklopke voor troontje,
jouw andere sympathieke medeleerlinge
en haar lovenswaardige poging ...
groetjes in vriendschap,
denook
maar ...
kan er geen kleine proficiat af voor lotte,
jouw sympathieke medeleerlinge
en haar juist antwoord,
en ... een schouderklopke voor troontje,
jouw andere sympathieke medeleerlinge
en haar lovenswaardige poging ...
groetjes in vriendschap,
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Duizend maal mea culpa , dat ik zo iets durf te vergeten !!! SORRY
Beste troontje ,
Vele dank voor uw moedig proberen een mooie tekening te maken , maar met zo een programma lukt dat niet . Daarvoor moet ge kunnen tekenen met een programma die werkt met vectoren .
Lieve Lotte ,
Ik denk dat het een typ fout is , maar het zijn wel de 2 maantjes i.p.v. de 2 kleine cirkels .
De beredenering was anders correct , proficiat !
Meester Denook ziet toch ook alles wat er in zijn klas gebeurd hé !
Vele Groetjes van Sloeberkebebo en tot binnen kort na het verlof .....
PS Ik wilde neutraal blijven t.o.v. mijn lieve klasgenoten , nogmaals SORRY
Beste troontje ,
Vele dank voor uw moedig proberen een mooie tekening te maken , maar met zo een programma lukt dat niet . Daarvoor moet ge kunnen tekenen met een programma die werkt met vectoren .
Lieve Lotte ,
Ik denk dat het een typ fout is , maar het zijn wel de 2 maantjes i.p.v. de 2 kleine cirkels .
De beredenering was anders correct , proficiat !
Meester Denook ziet toch ook alles wat er in zijn klas gebeurd hé !
Vele Groetjes van Sloeberkebebo en tot binnen kort na het verlof .....
PS Ik wilde neutraal blijven t.o.v. mijn lieve klasgenoten , nogmaals SORRY
Meten is weten - Carpe diem
-
falcon1 - Lid geworden op: 31 okt 2007, 12:46
- Locatie: De Panne - Midden-Limburg
Sorry dat ik hier effe binnen val, maar ik zit al jaren met een probleem. Niet zo zeer wiskundig, maar iets waar jullie misschien een oplossing voor weten. Ik ga proberen om het uit te leggen en aan jullie om te oordelen of ik ergens een fout maak in mijn redenering...
We leven hier op een aard(bol). De omtrek is ongeveer 40.000km.
Moest ik op de evenaar staan, dan leg ik die afstand af in 24 uur. Dit wil zeggen dat ik meedraai op de aarde aan een snelheid van 40.000 : 24 = 1666 km/u. (deze snelheid is zelfs groter dan die van het geluid!) Voor ons in België is de afstand die we op 24 u afleggen 12.000 km, en draaien we rond aan een snelheid van 12.000 : 24 = 500 km/u. Door de eskimo's die op de noordpool staan, draaien om hun as en bewegen zich aan 0 km/u.
Dan dacht ik even aan de middelpuntvliedende kracht die je op die drie plaatsen ondervindt... die op de evenaar zal veel groter zijn als die in België en praktisch niks op de noordpool....
Dus... moest ik op de weegschaal gaan staan op de evenaar, België of noordpool zou ik daar overal een verschillend gewicht hebben.
Je zou kunnen veronderstellen dat de mensen die op de evenaar zitten door deze middelpunt vliedende kracht zich meer onttrekken aan de zwaartekracht...
Je zou kunnen verder denken. Auto's op de evenaar worden minder aangetrokken door de aarde en verbruiken dus minder?
Zou dit fenomeen van invoed kunnen zijn op mens en dier?
We leven hier op een aard(bol). De omtrek is ongeveer 40.000km.
Moest ik op de evenaar staan, dan leg ik die afstand af in 24 uur. Dit wil zeggen dat ik meedraai op de aarde aan een snelheid van 40.000 : 24 = 1666 km/u. (deze snelheid is zelfs groter dan die van het geluid!) Voor ons in België is de afstand die we op 24 u afleggen 12.000 km, en draaien we rond aan een snelheid van 12.000 : 24 = 500 km/u. Door de eskimo's die op de noordpool staan, draaien om hun as en bewegen zich aan 0 km/u.
Dan dacht ik even aan de middelpuntvliedende kracht die je op die drie plaatsen ondervindt... die op de evenaar zal veel groter zijn als die in België en praktisch niks op de noordpool....
Dus... moest ik op de weegschaal gaan staan op de evenaar, België of noordpool zou ik daar overal een verschillend gewicht hebben.
Je zou kunnen veronderstellen dat de mensen die op de evenaar zitten door deze middelpunt vliedende kracht zich meer onttrekken aan de zwaartekracht...
Je zou kunnen verder denken. Auto's op de evenaar worden minder aangetrokken door de aarde en verbruiken dus minder?
Zou dit fenomeen van invoed kunnen zijn op mens en dier?
Elke dag is hetzelfde... alleen een beetje anders...
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste falcon de eerste,
het is allemaal veel eenvoudiger dan je laat uitschijnen.
- Als je op de kermis op een paardemolen zit en meedraait, dan zul je,
mocht je plots omhoog springen, daarna in een achterliggend wagentje
terechtkomen.
De molen draait verder en jij draait even niet volledig mee.
- De aarde die aan de evenaar 40 000 km aflegt (-draait-) in 24 uur;
legt dus op één seconde ongeveer 463 meter af.
Een hoogspringer die meer dan één seconde het contact met de aarde
verliest zou dan - zie paardemolen - 463 meter verder moeten neerkomen
dan waar hij de grond verliet. Dat is natuurlijk niet zo. We draaien mee,
voelen dat niet, blijven alleen één met de aarde.
Een vliegtuig dat op 3000 meter hoogte vliegt, hoort nog bij de aarde.
Als het windstil is en het vliegt met de draairichting van de aarde mee,
of vliegt tegen de draairichting in, zal met dezelfde motorenkracht op
gelijke tijdspannen dezelfde afstand worden afgelegd. Hij zal dus niet
meer weg afleggen (afvliegen) als hij met de draairichting meevliegt.
- Een gans ander voorbeeld.
Een vlieg in de keuken en een vlieg in een auto zal met dezelfde snel-
heid heen en weer vliegen, ook al rijdt de auto zelf tegen 120 km per uur
verder. De vlieg zal niet tegen de achterruit geplakt worden. Hier is de
wereld van de vlieg herleid tot de wereld van de auto.
- Je weet toch ook dat er een enorme kracht nodig is om de mens de
ruimte in te schieten. Hij moet heel ver worden gekatapulteerd om aan
de zwaartekracht onttrokken te worden.
Besluit beste falcon:
voor dergelijke en vele andere problemen ... blijven we best met de beide
voeten op de grond en plaatsen niet te veel vragen waar het niet nodig is
groetjes denook
ps. zien we falcon niet eens bij de wiskunde problemen?
volgende reeks op dinsdag 20 april
het is allemaal veel eenvoudiger dan je laat uitschijnen.
- Als je op de kermis op een paardemolen zit en meedraait, dan zul je,
mocht je plots omhoog springen, daarna in een achterliggend wagentje
terechtkomen.
De molen draait verder en jij draait even niet volledig mee.
- De aarde die aan de evenaar 40 000 km aflegt (-draait-) in 24 uur;
legt dus op één seconde ongeveer 463 meter af.
Een hoogspringer die meer dan één seconde het contact met de aarde
verliest zou dan - zie paardemolen - 463 meter verder moeten neerkomen
dan waar hij de grond verliet. Dat is natuurlijk niet zo. We draaien mee,
voelen dat niet, blijven alleen één met de aarde.
Een vliegtuig dat op 3000 meter hoogte vliegt, hoort nog bij de aarde.
Als het windstil is en het vliegt met de draairichting van de aarde mee,
of vliegt tegen de draairichting in, zal met dezelfde motorenkracht op
gelijke tijdspannen dezelfde afstand worden afgelegd. Hij zal dus niet
meer weg afleggen (afvliegen) als hij met de draairichting meevliegt.
- Een gans ander voorbeeld.
Een vlieg in de keuken en een vlieg in een auto zal met dezelfde snel-
heid heen en weer vliegen, ook al rijdt de auto zelf tegen 120 km per uur
verder. De vlieg zal niet tegen de achterruit geplakt worden. Hier is de
wereld van de vlieg herleid tot de wereld van de auto.
- Je weet toch ook dat er een enorme kracht nodig is om de mens de
ruimte in te schieten. Hij moet heel ver worden gekatapulteerd om aan
de zwaartekracht onttrokken te worden.
Besluit beste falcon:
voor dergelijke en vele andere problemen ... blijven we best met de beide
voeten op de grond en plaatsen niet te veel vragen waar het niet nodig is
groetjes denook
ps. zien we falcon niet eens bij de wiskunde problemen?
volgende reeks op dinsdag 20 april
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste iedereen,
vanavond als tussendoortje (-zoals ook sloeberkebebo-)
een merkwaardige vaststelling.
We weten allemaal, dat
als a<b en b<c dat dan steeds a<c.
Vanavond iets gelijkaardig maar dan een voorbeeld van
a>b en b>c en toch c>a.
Mooi, zeker lezen,
groetjes, denook
vanavond als tussendoortje (-zoals ook sloeberkebebo-)
een merkwaardige vaststelling.
We weten allemaal, dat
als a<b en b<c dat dan steeds a<c.
Vanavond iets gelijkaardig maar dan een voorbeeld van
a>b en b>c en toch c>a.
Mooi, zeker lezen,
groetjes, denook
-
falcon1 - Lid geworden op: 31 okt 2007, 12:46
- Locatie: De Panne - Midden-Limburg
Beste Denook, merciekes voor de uitleg.
het klopt wat je zegt, het een is met het ander verbonden en je moet alles in zijn vergelijk zien...
Er is ook nog iets als behoudt van energie... wat als ja van de paardemolen springt, of als je die vlieg uit je wagen gooit? Wat zou er gebeuren, moest de aarde plots stoppen?
Enfin, ik mag er niet aan denken, en zal ik ook niet meer doen..
Misschien dat ik beter eens een wiskundig vraagske ga (proberen) oplossen hier...
het klopt wat je zegt, het een is met het ander verbonden en je moet alles in zijn vergelijk zien...
Er is ook nog iets als behoudt van energie... wat als ja van de paardemolen springt, of als je die vlieg uit je wagen gooit? Wat zou er gebeuren, moest de aarde plots stoppen?
Enfin, ik mag er niet aan denken, en zal ik ook niet meer doen..
Misschien dat ik beter eens een wiskundig vraagske ga (proberen) oplossen hier...
Elke dag is hetzelfde... alleen een beetje anders...
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
doen falcon, doen,
er is steeds voor elk wat wils ...
en nu een eigenaardigheidje voor iedereen.
Het gaat om een spelletje met drie personen A, B en C,
die twee per twee spelen.
De kansrekening toont aan (en 't is JUIST), dat
- als A en B spelen, A meest wint,
- als B en C spelen, B meest wint, en ...
- als C en A spelen, C meest wint.
Merkwaardig toch - reken maar mee.
A, B en C maken ieder een dobbelsteen volgens de volgende gegevens.
Twee spelers gooien hun steen; het hoogste getal wint.
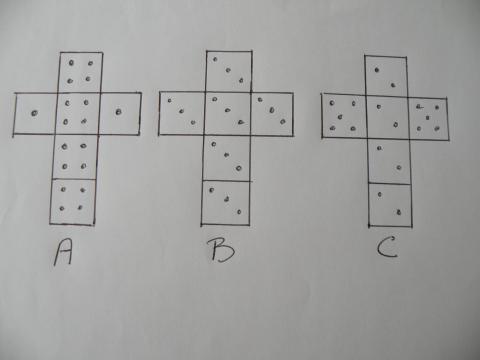
- als A en B spelen is de kans dat A wint:
4/6, want de dobbelsteen van A bevat 4 'vieren'
en die van B alleen drieën
A wint dus meer dan B
- als B en C spelen is de kans dat B wint:
4/6, want de dobbelsteen van C bevat 4 'tweeën
en die van B alleen drieën
B wint dus meer dan C
- en nu A en C:
als C een 'vijf' gooit wint hij, want de A-getallen zijn kleiner
C heeft twee 'vijven' dus reeds een kans van 2/6 om te winnen,
C wint ook als hij een 'twee' gooit en A en 'één ' gooit,
kans voor een 'twee' bij C: 4/6
kans voor een 'één' bij A: 2/6
kans voor beiden terzelfdertijd: 4/6 . 2/6 = 8/36 = 2/9
de kans dat C dus wint van A is 2/6 + 2/9 = 1/3 + 2/9 = 3/9 + 2/9 = 5/9
of C wint dus meer dan A.
Besluit:
A wint meer dan B,
B wint meer dan C en
C wint meer dan A
tot vandaag over één week voor een echte reeks
' problemen en probleempjes'
tot dan,
groetjes, denook
er is steeds voor elk wat wils ...
en nu een eigenaardigheidje voor iedereen.
Het gaat om een spelletje met drie personen A, B en C,
die twee per twee spelen.
De kansrekening toont aan (en 't is JUIST), dat
- als A en B spelen, A meest wint,
- als B en C spelen, B meest wint, en ...
- als C en A spelen, C meest wint.
Merkwaardig toch - reken maar mee.
A, B en C maken ieder een dobbelsteen volgens de volgende gegevens.
Twee spelers gooien hun steen; het hoogste getal wint.
- als A en B spelen is de kans dat A wint:
4/6, want de dobbelsteen van A bevat 4 'vieren'
en die van B alleen drieën
A wint dus meer dan B
- als B en C spelen is de kans dat B wint:
4/6, want de dobbelsteen van C bevat 4 'tweeën
en die van B alleen drieën
B wint dus meer dan C
- en nu A en C:
als C een 'vijf' gooit wint hij, want de A-getallen zijn kleiner
C heeft twee 'vijven' dus reeds een kans van 2/6 om te winnen,
C wint ook als hij een 'twee' gooit en A en 'één ' gooit,
kans voor een 'twee' bij C: 4/6
kans voor een 'één' bij A: 2/6
kans voor beiden terzelfdertijd: 4/6 . 2/6 = 8/36 = 2/9
de kans dat C dus wint van A is 2/6 + 2/9 = 1/3 + 2/9 = 3/9 + 2/9 = 5/9
of C wint dus meer dan A.
Besluit:
A wint meer dan B,
B wint meer dan C en
C wint meer dan A
tot vandaag over één week voor een echte reeks
' problemen en probleempjes'
tot dan,
groetjes, denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
Paasverlof voorbij, dus weer nieuwe wislundige problemen en
probleempjes,
hier gaan we.
1) In een familie zijn broers en zussen.
Elk meisje heeft evenveel broers als zussen.
Elke jongen heeft tweemaal zoveel zussen als broers.
Hoe ziet de familie er uit?
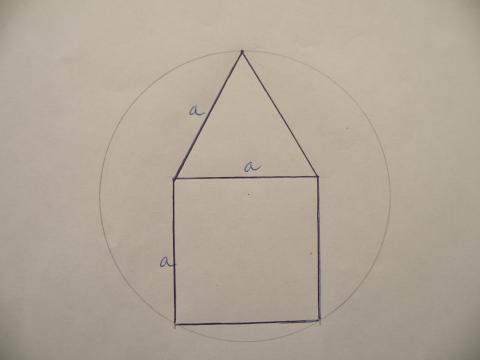
2) In een cirkel tekenen we een vierkant met zijde a en twee hoekpunten
op de cirkel gelegen.
Boven het vierkant past nog een gelijkzijdige driehoek waarvan de top
ook op de cirkel ligt.
Bereken de straal van de cirkel in functie van a.
3) In een vlak tekenen we n rechten.
Geen twee rechten zijn evenwijdig.
Geen drie rechten gaan door éénzelfde punt.
In hoeveel stukken zal het vlak worden verdeeld door de n rechten?
Tip: tel bij 0, 1, 2, 3, 4, ... rechten het aantal stukken
en tracht daaruit een algemene formule te vinden voor n rechten.
4) 3 appels, 2 bananen en 1 citroen kosten samen 3,90.
1 appel, 4 bananen en 2 citroenen kosten samen 4,80.
Hoeveel kosten 3 appels, 4 bananen en 2 citroenen samen?
5) In 36 seconden zaagt men een boomstam in 4 stukken.
Hoe lang duurt het om de boomstam in 5 stukken te zagen?
6) Hoe koop je met 10 euro precies enkele postzegels van 80 cent,
driemaal zoveel postzegels van 90 cent en voor de rest, postzegels
van één euro?
7) Vul in met of -,
a) 7 ... 4 ... 8 ... 3 ... 5 ... 1 = 10
b) 6 ... 4 ... 5 ... 9 ... 7 ... 1 = 20
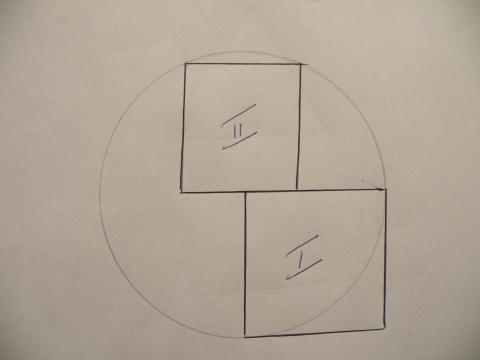
8 ) Vierkant I heeft twee zijden die samenvallen met de straal van
een cirkel.
Vierkant II heeft twee hoekpunten op dezelfde cirkel en steunt op
vierkant I.
Bereken de verhouding: Oppervlakte I / Oppervlakte II = ...
9) Nog maar eens ...
A, B en C zijn cijfers waar we getallen mee schrijven.
Nu is AB + AB + AB + AB = CA.
Zoek de cijfers A, B en C.
10) Iets moeilijker om te eindigen.
Een reservoir ontvangt continu water: i liter per uur.
Er zijn ook onderaan afvoerpijpen die (- als ze open staan -),
per pijp u liter laten weglopen.
Bij 10 open afvoerpijpen loopt het reservoir leeg in 2 uur en 30 minuten,
bij 6 open afvoerpijpen loopt het leeg in 5 uur en 30 minuten,
bij 3 open afvoerpijpen loopt het leeg in ??? uur en ??? minuten.
We zijn er weer door.
Succes iedereen, ook eventueel nieuwe spelers.
Deze laatsten lezen eerst blz 1 - daar staat een reglement(je),
tot morgen,
denook
probleempjes,
hier gaan we.
1) In een familie zijn broers en zussen.
Elk meisje heeft evenveel broers als zussen.
Elke jongen heeft tweemaal zoveel zussen als broers.
Hoe ziet de familie er uit?
2) In een cirkel tekenen we een vierkant met zijde a en twee hoekpunten
op de cirkel gelegen.
Boven het vierkant past nog een gelijkzijdige driehoek waarvan de top
ook op de cirkel ligt.
Bereken de straal van de cirkel in functie van a.
3) In een vlak tekenen we n rechten.
Geen twee rechten zijn evenwijdig.
Geen drie rechten gaan door éénzelfde punt.
In hoeveel stukken zal het vlak worden verdeeld door de n rechten?
Tip: tel bij 0, 1, 2, 3, 4, ... rechten het aantal stukken
en tracht daaruit een algemene formule te vinden voor n rechten.
4) 3 appels, 2 bananen en 1 citroen kosten samen 3,90.
1 appel, 4 bananen en 2 citroenen kosten samen 4,80.
Hoeveel kosten 3 appels, 4 bananen en 2 citroenen samen?
5) In 36 seconden zaagt men een boomstam in 4 stukken.
Hoe lang duurt het om de boomstam in 5 stukken te zagen?
6) Hoe koop je met 10 euro precies enkele postzegels van 80 cent,
driemaal zoveel postzegels van 90 cent en voor de rest, postzegels
van één euro?
7) Vul in met of -,
a) 7 ... 4 ... 8 ... 3 ... 5 ... 1 = 10
b) 6 ... 4 ... 5 ... 9 ... 7 ... 1 = 20
8 ) Vierkant I heeft twee zijden die samenvallen met de straal van
een cirkel.
Vierkant II heeft twee hoekpunten op dezelfde cirkel en steunt op
vierkant I.
Bereken de verhouding: Oppervlakte I / Oppervlakte II = ...
9) Nog maar eens ...
A, B en C zijn cijfers waar we getallen mee schrijven.
Nu is AB + AB + AB + AB = CA.
Zoek de cijfers A, B en C.
10) Iets moeilijker om te eindigen.
Een reservoir ontvangt continu water: i liter per uur.
Er zijn ook onderaan afvoerpijpen die (- als ze open staan -),
per pijp u liter laten weglopen.
Bij 10 open afvoerpijpen loopt het reservoir leeg in 2 uur en 30 minuten,
bij 6 open afvoerpijpen loopt het leeg in 5 uur en 30 minuten,
bij 3 open afvoerpijpen loopt het leeg in ??? uur en ??? minuten.
We zijn er weer door.
Succes iedereen, ook eventueel nieuwe spelers.
Deze laatsten lezen eerst blz 1 - daar staat een reglement(je),
tot morgen,
denook
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
2) In een cirkel tekenen we een vierkant met zijde a en twee hoekpunten
op de cirkel gelegen. Boven het vierkant past nog een gelijkzijdige driehoek waarvan de top ook op de cirkel ligt. Bereken de straal van de cirkel in functie van a.
Diameter van de cirkel is : a + √a²- √ (a/2)² = a + a – a/2 = 3a/2.
Straal van de cirkel is 3a/4.
op de cirkel gelegen. Boven het vierkant past nog een gelijkzijdige driehoek waarvan de top ook op de cirkel ligt. Bereken de straal van de cirkel in functie van a.
Diameter van de cirkel is : a + √a²- √ (a/2)² = a + a – a/2 = 3a/2.
Straal van de cirkel is 3a/4.
Sudoku, wijntjes proeven, genieten.