Wiskundige problemen en probleempjes 2 - Pagina 34 — Forum

pastoor 23 apr 2010, 18:14 Hoeselt, White House 14.651 berichten

Denook,

Ik had 55.
Maar ik kon dat niet geloven, omwille van het verschil met de twee andere.
De gebruikte methode was ongeveer dezelfde maar niet helemaal juist, en de massa's waren niet gelijk.
Ik deed het op basis van 1 afvoerpijp, en dat is niet goed, het is beter het te behandelen op het totale volume water ... en dan zijn de M's gelijk.

Dit is wat ik geschreven had:

Vraag 10) Iets moeilijker om te eindigen. Een reservoir ontvangt continu water: i liter per uur. Er zijn ook onderaan afvoerpijpen die (- als ze open staan -), per pijp u liter laten weglopen. Bij 10 open afvoerpijpen loopt het reservoir leeg in 2 uur en 30 minuten, bij 6 open afvoerpijpen loopt het leeg in 5 uur en 30 minuten, bij 3 open afvoerpijpen loopt het leeg in ??? uur en ??? minuten.

Met 10 afvoerpijpen is het reservoir ledig in 2,5 uren.
Door 1 afvoerpijp loopt (1/10) van het water, per uur is dat (2/50).
Er komt i liter per uur bij, via 1 afvoerpijp loopt (i/10) liter/uur weg.
Door 1 afvoerpijp loopt er u liter water/uur weg, u = (2/50) + (i/10).
Vergelijking (1) u = (2 + 5i)/50.

Met 6 afvoerpijpen is het reservoir ledig in 5,5 uren.
Door 1 afvoerpijp loopt (1/6) van het water, per uur is dat (2/66).
Er komt i liter per uur bij, via 1 afvoerpijp loopt er (i/6) liter/uur weg.
Door 1 afvoerpijp loopt er u liter water/uur weg. u = (2/66) + (i/6).
Vergelijking (2) u = (2 + 11i)/66 .

Met 3 afvoerpijpen is het reservoir ledig na x uren.
Door 1 afvoerpijp loopt (1/3) van het water, per uur is dat (1/3x).
Er komt i liter per uur bij, via 1 afvoerpijp loopt er (i/3) liter/uur weg.
Door 1 afvoerpijp loopt er u liter water/uur weg. u = (1/3x) + (i/3).
Vergelijking (3) u = 1/3x+ i/3.

Uit vergelijking (1) en (2) kan men i bepalen.
(2 + 5i)/50 = (2 + 11i)/66 of (132 + 330i) = (100 + 550i).
Of 220i = 32, en i = 32/220.
Vergelijking (4) i = 8/55.

Uit vergelijking (1), (3) en (4) volgt: (2 + 5i)/50 = (i/3 + 1/3x), met (i = 8/55).
Of (2 + 5(8/55))/50 = (8/55)/3 + 1/3x.
Na uitwerking levert dat x = 55.

Oplossing: het reservoir met 3 afvoerpijpen is ledig na 55 uren.
En dat geloof ik niet. Zoek de fout.

Ik ga het eens vergelijken met uw oplossing.

Sudoku, wijntjes proeven, genieten.

sloeberkebebo 25 apr 2010, 17:32 Roeselare 251 berichten

Hallo allemaal

Hier een tussendoortje
Als:
2 + 3 = 10
7 + 2 = 63
6 + 5 = 66
8 + 4 = 96
Dan is:
9 + 7 = ????

Groetjes Sloeber

Meten is weten - Carpe diem

lotte 25 apr 2010, 21:39 Tielt 6.226 berichten

dag sloeber

kan het : 144 ?

groetjes
lotte.

sloeberkebebo 26 apr 2010, 09:36 Roeselare 251 berichten

Lieve Lotte ,

't Is helemaal just .
mvg

Sloeber

Als:
2 + 3 = 10 .......2*2=4 .....+.....3*2=6 ......=> 10
7 + 2 = 63.......7*7=49.....+.....2*7=14.....=> 63
6 + 5 = 66.......6*6=36.....+.....5*6=30.....=> 66
8 + 4 = 96 ......8*8=64......+.....4*8=32.....=> 96
Dan is:
9 + 7 =144......9*9=81.....+......7*9=63....=>144

Meten is weten - Carpe diem

pastoor 27 apr 2010, 12:09 Hoeselt, White House 14.651 berichten

Misschien iets sneller telbaar.
(2 + 3) * 2 = 10
(7 + 2) * 7 = 63
(6 + 5) * 6 = 66
(8 + 4) * 8 = 96
(9 + 7) * 9 =144

Sudoku, wijntjes proeven, genieten.

oomski 29 apr 2010, 11:58 Thuis. 593 berichten

Ik had ook de methode van pastoor er in gezien.

Wie op wraak zint, houdt zijn eigen wonden open.

denook Startte dit onderwerp 04 mei 2010, 20:00 Vlaams-Brabant 1.870 berichten

Wiskundige problemen en probleempjes van 4 mei 2010,

1)In een rechthoek zijn de lengte en de breedte natuurlijke getallen, zó dat de omtrek in cm gelijk is aan de oppervlakte in cm². Bereken de afmetingen.

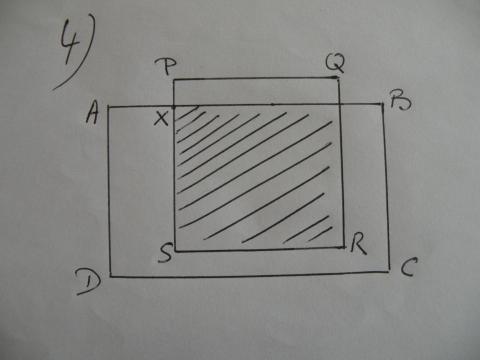
Afbeelding

Dit zijn de hoekpunten van een regelmatige zeshoek.
Door sommige van die punten te verbinden ontstaan figuren.
Welke van volgende figuren kan men zo niet bekomen?
A vierkant, B) trapezium, C) scherphoekige driehoek,
D) rechthoekige driehoek, D) stomphoekige driehoek.

3) Gegeven: twee natuurlijke getallen.
Als je weet dat de som van:
de som van de getallen en het verschil van de getallen en het product van de getallen en het quotiënt van de getallen 243 is ... over welke twee natuurlijke getallen gaat het dan?

Afbeelding

Als ABCD een rechthoek is met afmetingen 10 en 6 en PQRS een vierkant met zijde 6 en de oppervlakte van het gearceerde gebied is de helft van ABCD, wat is dan de afstand van P tot X?

5) De rekenmachine van pastoor is stuk; je kan de '1' niet zien.
Als hij 3141 intikt leest hij het getal 34 zonder tussenruimten.
Pastoor tikt een getal in van zes cijfers en leest 2090.
Hoeveel verschillende getallen kan pastoor dan getypt hebben?

6) Een kip kost 10 euro, een haan 3 euro en een kuiken 0,5 euro.
Voor 100 euro koop ik precies 100 dieren. Hoeveel van elke soort?

7) De leerlingen van de klas willen een geschenk kopen.
Als ze ieder m euro geven, hebben ze een overschot van n euro.
Als ze ieder p euro geven, hebben ze een tekort van q euro.
Hoeveel leerlingen zitten er in de klas?

8 ) kx - 12 = 3k is een vergelijking in x, en k is een vast gekozen getal.
Als de oplossing x een geheel getal moet zijn, hoeveel waarden kan men
dan kiezen voor k?

9) Een kubus wordt volledig rood geverfd en dan verdeeld in 125 even grote klein kubusjes. Hoeveel van deze kleine kubusjes hebben geen enkel gekleurd zijvlak?

10) Iemand antwoordde me ooit op de vraag "hoe oud hij was?", het volgende:
"eergisteren was ik 62 jaar en volgend jaar word ik 65 jaar."
De man scheen nog gelijk te hebben ook ... Verklaar.

Succes iedereen. Nieuwe leerlingen (-welkom!!-) lezen eerst blz. 1.
Tot morgen, denook

lotte 04 mei 2010, 20:03 Tielt 6.226 berichten

Goeie avond denook

vraag 9
antw. elke ribbe van de grote kubus omvat vijf ribben
van de kleine kubussen.
Alleen de binnenste kleine kubusjes zijn niet geverfd,
dat zijn er 3 x 3 x 3 of 27.
groetjes allen
lotte.

sloeberkebebo 04 mei 2010, 20:18 Roeselare 251 berichten

Vraag 4

ABCD=10*6=60
PQRS=6*6=36
PX=1

Sloeber

Meten is weten - Carpe diem

pastoor 04 mei 2010, 20:18 Hoeselt, White House 14.651 berichten

Goede avond Denook en de anderen.

1)In een rechthoek zijn de lengte en de breedte natuurlijke getallen, zó dat de omtrek in cm gelijk is aan de oppervlakte in cm². Bereken de afmetingen.

omtrek = 2L + 2B = oppervlakte = LB

2 = (LB)/(L + B)

antwoord: L = 4, B = 4

Sudoku, wijntjes proeven, genieten.

oomski 05 mei 2010, 13:35 Thuis. 593 berichten

Goedemiddag,

Vraag 2:

A, het vierkant kan men niet bekomen.

Wie op wraak zint, houdt zijn eigen wonden open.

troontje 05 mei 2010, 13:45 2.351 berichten

goede middag iedereen,

vraag6

5x10=50 € voor ( 5 kippen)
1x3 =3 € voor(1 haan)
94x0.5=47€voor(94 kuikens)

5+1+94+100 dieren
50+3+47+100 euro's

troontje,

denook Startte dit onderwerp 05 mei 2010, 19:46 Vlaams-Brabant 1.870 berichten

goede avond iedereen,

alle leerlingen kwamen weer aan bod
en bijna alles was ook weer juist,
hier gaan we

vraag 9) Lotte - ok

vraag 4) Sloeberkebebo - ok

vraag 1) Pastoor - bijna ok
je stopte bij 2 = LB/(L+B),
hieruit haalde je L = 4 en B = 4
dat is juist, doch er is nog een oplossing,
die zie je beter als je op een andere manier verder rekent:
2L + 2B = LB
2B - LB = -2L
(2 - L)B = - 2l
B = -2L/(2 - L)
B = 2L/(L - 2)
deze laatste vorm moet een natuurlijk getal zijn,
of (L-2) is een deler van 2L
dat is zo voor L = 3, 4 en 6;
daarna gaat dat niet meer
dus antwoorden:
L = 3 en dan B = 6
L = 4 en dan B = 4 (jouw antwoord)
L = 6 en dan B = 3
de eerste en derde oplossing zijn natuurlijk dezelfde

vraag 2) Oomski -ok

vraag 6) Troontje - ok
één haan bij vijf kippen, zo hoort het op een gezond boerenerf

blijven over: 3 (niet gemakkelijk), 5, 7, 8 en 9(even redeneren)

tot morgen, denook

lotte 05 mei 2010, 20:03 Tielt 6.226 berichten

10) Iemand antwoordde me ooit op de vraag "hoe oud hij was?", het volgende:
"eergisteren was ik 62 jaar en volgend jaar word ik 65 jaar."
De man scheen nog gelijk te hebben ook ... Verklaar.

“ooit” was op l januari
eergisteren30 december was hij nog 62 jaar
gisteren 31 december – verjaardag - 63 jaar
dit jaar op 31 december 64 jaar
het daarop volgend jaar 65 jaar

groetjes allen
lotte.

pastoor 05 mei 2010, 21:08 Hoeselt, White House 14.651 berichten

Vraag 5) De rekenmachine van pastoor is stuk; je kan de '1' niet zien.
Als hij 3141 intikt leest hij het getal 34 zonder tussenruimten. Pastoor tikt een getal in van zes cijfers en leest 2090. Hoeveel verschillende getallen kan pastoor dan getypt hebben?
112090, 121090, 120190, 120910, 120901.
211090, 210190, 210910, 310901.
201190, 201910, 201901.
209110, 209101.
209011

Antwoord: 15 mogelijkheden.

Sudoku, wijntjes proeven, genieten.