Wiskundig probleem
-
Wil. - Lid geworden op: 15 nov 2005, 19:41
Je zit vast in je denken: je beziet het als een situatie waarin slecht 2 bekers (of dozen) betrokken zijn. Dáár zit je probleem. Zolang je deze opgave niet bekijkt als een situatie van 2 kansen tegen 1 kans, ga je dit niet doorgronden.Dicksy schreef: ↑15 aug 2023, 00:41Dat zou aan een test kunnen onderworpen worden met dezelfde speler met het fameuze balletje balletje spel.Door veelvuldig dit spel te spelen komt de kracht van het statistisch voordeel bovendrijven en blijkt dat wisselen meer keren (niet altijd!) tot winst leidt.
- 3 bekers gelabeld A,B en C.waaronder één een erwt.
- 1 beker zonder erwt wordt omgedraaid en de kandidaat mag dan gokken onder welk van de twee resterende bekers de erwt zit.
Zijn voorkeur moet niet geweten zijn want dan verliest hij altijd.
- 20x herhalen en noteren 1x per dag gedurende 1 week bv.
De kans blijft voor mij even groot dat hij na 1 week meer mis gegokt heeft als dat de kans even groot is dat hij na 1 week meer juist gegokt heeft.
Als ik je spel met de bekers juist begrepen heb, dan maakt de speler zijn eerste keuze niet bekend. Dat moet nochtans wel gebeuren, zodat degene die de erwt onder de beker gestopt heeft ook één lege beker van de twee overgebleven bekers kan omdraaien. De speler moet enkel aanwijzen welke van de 3 bekers volgens hem de erwt bevat; die beker wordt vanzelfsprekend niet omgedraaid.
Het spel moet op gelijke manier verlopen als het spel met de dozen.
-
E.T. - Lid geworden op: 11 nov 2008, 21:15
De sleutel zit "at random" in een van de TWEE dozen, de derde doos is en blijft leeg
Of de quizkandidaat kiest of wisselt maakt niet uit, de sleutel blijft waar hij is, toch?
WE WACHTEN

Of de quizkandidaat kiest of wisselt maakt niet uit, de sleutel blijft waar hij is, toch?
De vraag is om in heel gewone taal uit te leggen waarom hij meer kans maakt om te winnen als hij van mening verandert.
WE WACHTEN
OPGELET bovenstaande tekst kan sporen van ironie en/of sarcasme bevatten
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
-
Dicksy - Lid geworden op: 11 jul 2019, 20:17
Of het nu met die bekers is of met die dozen:Als ik je spel met de bekers juist begrepen heb, dan maakt de speler zijn eerste keuze niet bekend. Dat moet nochtans wel gebeuren, zodat degene die de erwt onder de beker gestopt heeft ook één lege beker van de twee overgebleven bekers kan omdraaien. De speler moet enkel aanwijzen welke van de 3 bekers volgens hem de erwt bevat; die beker wordt vanzelfsprekend niet omgedraaid.
Het spel moet op gelijke manier verlopen als het spel met de dozen.
De 'finale' begint met 3 dozen, A,B en C waaruit de kandidaat de sleutel van de auto moet kunnen proberen aan te duiden, kans 1 op 3.
De quizmaster doet een geste en opent doos C, perfect wetende dat dit een lege doos is. De kandidaat blij want zijn kansen stijgen van 1 op 3 naar 1 op 2. Die doos C bestaat niet meer in het spel, is weg, foetsie en daar dient geen rekening meer gehouden te houden door de kandidaat. Was doos C zijn voorkeur en de quizmaster opent die doos, goed wetende dat die leeg, weer een meevaller voor de kandidaat.
Voor hem tellen nu nog 2 dozen, dus 1 kans op 2 dat hij de juiste doos opent maar ook 1 kans op 2 dat hij de verkeerde doos opent.
Als hij in eerste instantie (bij 3 dozen) voor doos C zou kiezen (zijn buikgevoel zeg maar) is dat voor hem een meevaller want hij zou al direct verloren hebben, geen sleutel. Als hij in eerste instantie (bij 3 dozen) voor doos A zou gekozen hebben versterkt dat zijn eerste keus omdat doos C geopend werd en leeg was. De kans bestaat dus dat hij hier het bij het rechte eind heeft maar de kans bestaat ook dat zijn aanvoelen (buikgevoel) verkeerd is en de sleutel in doos B zit. Het blijft 50/50.
De quizmaster mag dan nog het voorgevoel van de kandidaat kennen of niet, hij zal altijd die doos openen die leeg is.
Men kan dit spel herhalen zoveel men wil en of men nu van gedacht wisselt of niet in zijn keuze vergroot de kans helemaal niet dat hij het meer gaat winnen dan verliezen, de kans is er ook dat hij het meer gaat verliezen dan winnen. Het blijft gewoon 1 kans op 2, winst of verlies.
Zo, nu stop ik erover.
-
Wil. - Lid geworden op: 15 nov 2005, 19:41
Natuurlijk blijft de sleutel waar hij was. Ik heb vanaf het begin gezegd dat het geen truc is.
Gisteren geschreven en volgens mij in heel eenvoudige bewoordingen uitgelegd:WE WACHTENDe vraag is om in heel gewone taal uit te leggen waarom hij meer kans maakt om te winnen als hij van mening verandert.
Als je één keuze mag maken uit de 3 gelijkaardige dozen, dan heb je 1 kans op 3 dat je juist kiest. Dat betekent dat in de resterende dozen – hier B en C – nog 2/3 van de kansen verborgen zit.
Wanneer de gastheer van de show dan één doos ‘uitschakelt’ door een lege doos te openen – veronderstel C - dan blijft de groep (B + C) samen toch 2/3 van de kansen bezitten.
Wanneer de kandidaat wisselt van A (zijn eerste keus) naar B, dan heeft hij geen zekerheid dat hij de autosleutel kiest, maar zijn kansen stijgen wel van 1 op 3 naar 2 kansen op 3. Het is nog altijd perfect mogelijk dat de sleutel in doos A zat, maar het ging erom de kansen te verhogen.
Het punt is dat je in een verkeerde denkmodus blijft zitten. Je beschouwt die laatste 2 overgebleven dozen als "de keuze". Dat is niet zo. Indien de kandidaat bij zijn eerste keuze blijft, dan blijft hij met 1 kans op 3 zitten. Het wordt zelfs niet 1 op 2.
Ik weet uit eigen ervaring dat dit tegen je intuïtie ingaat, maar dat is al eens eerder het geval geweest, herinner je je nog?
Het is een kwestie van logica en de zaak ten gronde dóórdenken, niet van intuïtie.
-
E.T. - Lid geworden op: 11 nov 2008, 21:15
E.T. schreef: ↑08 aug 2023, 08:09Ik ben nogal voor de theorie van 50/50
je wint of je wint niet
Maar dat dat helemaal niet juist is en een beetje kinderachtig is mij hier al meermaals uitgelegd LOL
Over de dozen nu:
als de sleutel niet in C zit dan wijzigt de situatie van
keuze uit 3 dozen naar
keuze uit 2 dozen
wisselen is dus zeker geen nadeel
OPGELET bovenstaande tekst kan sporen van ironie en/of sarcasme bevatten
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
-
Wil. - Lid geworden op: 15 nov 2005, 19:41
Je lijkt hier een verkeerde veronderstelling te maken. Kiest hij initieel voor C, dan zal de quizmaster één van de overgebleven dozen [A+B] openen en meer bepaald een lege. De quizmaster weet immers in welke doos de sleutel zit. Hij opent altijd een lege doos.
De combinatie [A+B] bevat nu 2 kansen op 3.
-
Wil. - Lid geworden op: 15 nov 2005, 19:41
ET, je moet verklaren waarom hij veel meer kansen heeft als hij wisselt. Zijn kansen verdubbelen zelfs!E.T. schreef: ↑15 aug 2023, 12:30E.T. schreef: ↑08 aug 2023, 08:09Ik ben nogal voor de theorie van 50/50
je wint of je wint niet
Maar dat dat helemaal niet juist is en een beetje kinderachtig is mij hier al meermaals uitgelegd LOL
Over de dozen nu:
als de sleutel niet in C zit dan wijzigt de situatie van
keuze uit 3 dozen naar
keuze uit 2 dozen
wisselen is dus zeker geen nadeel
De stelling 'het is zeker geen nadeel als hij wisselt' geraakt niet verder dan een 50/50 situatie: zijn eerste keuze heeft volgens jouw visie dan evenveel kans als veranderen van keuze, en dat klopt niet.
Je laat nog steeds je intuïtie de bovenhand nemen.
Laatst gewijzigd door Wil. op 15 aug 2023, 13:58, 1 keer totaal gewijzigd.
-
E.T. - Lid geworden op: 11 nov 2008, 21:15
Elk nadeel heeft z´n voordeel, toch?
Jij blijft er van uit gaan dat
A = 1/3
B+C = 1/3 + 1/3 = 2/3 FOUT
B+C = 1/3 + 0 = 1/3
Jij blijft er van uit gaan dat
A = 1/3
B+C = 1/3 + 1/3 = 2/3 FOUT
B+C = 1/3 + 0 = 1/3
Laatst gewijzigd door E.T. op 15 aug 2023, 13:00, 1 keer totaal gewijzigd.
OPGELET bovenstaande tekst kan sporen van ironie en/of sarcasme bevatten
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
-
Dicksy - Lid geworden op: 11 jul 2019, 20:17
Hij blijft inderdaad bij zijn kans 1 op 3 zitten zolang die lege doos (C) niet geopend wordt door de quizmaster. Daar waar hij eerder 1 kans op winst en 2 kansen op een mislukking had is die kans op een mislukking nu verkleint tot 1 kans.door Wil. » 14 minuten geleden
Het punt is dat je in een verkeerde denkmodus blijft zitten. Je beschouwt die laatste 2 overgebleven dozen als "de keuze". Dat is niet zo. Indien de kandidaat bij zijn eerste keuze blijft, dan blijft hij met 1 kans op 3 zitten. Het wordt zelfs niet 1 op 2.
Doos C speelt niet meer mee vanaf het moment dat ze geopend werd. Drie kleine dozen A,B en C. Kleine doos C werd geopend en was leeg, toen waren ze nog met twee. Twee kleine dozen A en B enz.........
-
E.T. - Lid geworden op: 11 nov 2008, 21:15
Wil, je blijft er van uit gaan dat
A = 1/3
B+C = 1/3 + 1/3 = 2/3
echter
B+C = 1/3 + 0 = 1/3
A = B
A = 1/3
B+C = 1/3 + 1/3 = 2/3
echter
B+C = 1/3 + 0 = 1/3
A = B
OPGELET bovenstaande tekst kan sporen van ironie en/of sarcasme bevatten
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
-
Wil. - Lid geworden op: 15 nov 2005, 19:41
Goed. Ik merk dat jullie vastzitten in een denkpatroon.
Ik ga harder bewijsmateriaal naar voor brengen waaruit duidelijker zal blijken dat de praktijk je ongelijk geeft.
We veronderstellen - zoals in ons vertrekpunt - dat de kandidaat in de 3 gevallen hieronder steeds opteert voor doos A. (met een eerste keuze voor B of voor C verandert er aan de uitkomst niets, maar we overlopen de mogelijkheden wanneer voor A wordt gekozen). De quizmaster opent altijd één van de overgebleven dozen en natuurlijk opent hij de lege. Ze kunnen beide leeg zijn maar ook dan opent de quizmaster één lege doos.
De sleutel kan in doos A zitten, in doos B zitten of in doos C zitten.
Eerst bekijken we de situatie waarbij de kandidaat altijd beslist om te wisselen. Wat zijn de 3 mogelijke uitkomsten? Deze:

Je merkt dat de kandidaat in 1 geval verliest, maar in 2 gevallen wint hij door te veranderen. Dat is helemaal in overeenstemming met wat ik zei: hij heeft 2 kansen op 3 als hij wisselt.
Wat dan als hij bij zijn keuze blijft? Ook hier zijn er 3 mogelijkheden: de sleutel kan in doos A zitten, in doos B zitten of in doos C zitten.
De kandidaat maakt keuze A. De quizmaster opent een lege doos van het groepje [B+C] maar toch houdt de kandidaat voet bij stuk. Hij denkt dat hij 50% kans heeft, om het even in welke van de 2 'kanshebbende dozen' - althans in zijn denkwijze - de sleutel zich bevindt.
Hier de 3 mogelijke uitkomsten:
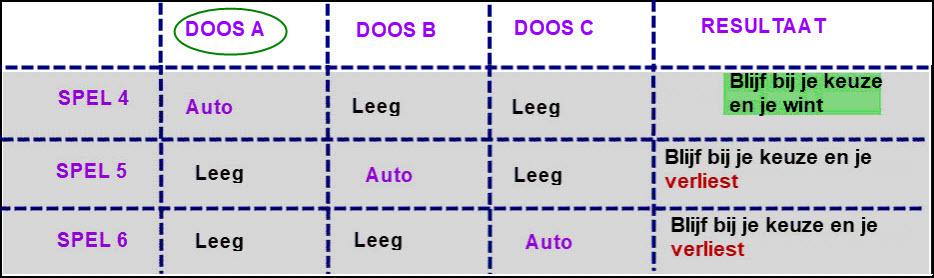
Zoals je ziet zijn er nu 2 van de 3 mogelijkheden waarbij de kandidaat verliest en dit bij niet wisselen.
In 1 geval op 3 wint hij.
Besluit? Door deze tabel van logische mogelijkheden op te stellen, blijkt dat wisselen van keuze de kans sterk vergroot.
Door bij de eerste keuze te blijven, blijft er ook maar 1 kans op 3 om de auto te winnen.
Ik ga harder bewijsmateriaal naar voor brengen waaruit duidelijker zal blijken dat de praktijk je ongelijk geeft.
We veronderstellen - zoals in ons vertrekpunt - dat de kandidaat in de 3 gevallen hieronder steeds opteert voor doos A. (met een eerste keuze voor B of voor C verandert er aan de uitkomst niets, maar we overlopen de mogelijkheden wanneer voor A wordt gekozen). De quizmaster opent altijd één van de overgebleven dozen en natuurlijk opent hij de lege. Ze kunnen beide leeg zijn maar ook dan opent de quizmaster één lege doos.
De sleutel kan in doos A zitten, in doos B zitten of in doos C zitten.
Eerst bekijken we de situatie waarbij de kandidaat altijd beslist om te wisselen. Wat zijn de 3 mogelijke uitkomsten? Deze:

Je merkt dat de kandidaat in 1 geval verliest, maar in 2 gevallen wint hij door te veranderen. Dat is helemaal in overeenstemming met wat ik zei: hij heeft 2 kansen op 3 als hij wisselt.
Wat dan als hij bij zijn keuze blijft? Ook hier zijn er 3 mogelijkheden: de sleutel kan in doos A zitten, in doos B zitten of in doos C zitten.
De kandidaat maakt keuze A. De quizmaster opent een lege doos van het groepje [B+C] maar toch houdt de kandidaat voet bij stuk. Hij denkt dat hij 50% kans heeft, om het even in welke van de 2 'kanshebbende dozen' - althans in zijn denkwijze - de sleutel zich bevindt.
Hier de 3 mogelijke uitkomsten:

Zoals je ziet zijn er nu 2 van de 3 mogelijkheden waarbij de kandidaat verliest en dit bij niet wisselen.
In 1 geval op 3 wint hij.
Besluit? Door deze tabel van logische mogelijkheden op te stellen, blijkt dat wisselen van keuze de kans sterk vergroot.
Door bij de eerste keuze te blijven, blijft er ook maar 1 kans op 3 om de auto te winnen.
-
E.T. - Lid geworden op: 11 nov 2008, 21:15
Dat was de probleemstelling, C is leeg. Dus uw SPEL 3 en SPEL 6 zijn niet van toepassing.Wil. schreef: ↑08 aug 2023, 00:01Volg even de probleemstelling hieronder:
... Hij kiest doos A maar alvorens die doos te openen, doet de kwismaster, die goed weet in welke doos de sleutel zit, iets speciaals: hij opent doos C en laat zien dat er niets in die doos zit. Ze is leeg.
En nu stelt hij aan de kwiskandidaat de vraag of hij bij zijn keuze A blijft, want hij mag nu nog van gedacht veranderen aangezien doos A is toch nog niet geopend, en voor doos B kiezen. De kandidaat weet niet of de eerste doos de sleutel van die prachtige auto bevat. Hij weet nu enkel dat de sleutel niet in doos C zit ...
Nu schrijf je dat de quizmaster altijd de lege doos kiest ... maakt niet uit hé, je spel 2 en 3 zijn hetzelfde net zoals 5 en 6
Ergens schrijf je ook dat als je duizend keer je kop of munt speelt het resultaat ongeveer 50/50 zal zijn dat mag jij dan wel geloven maar daar is geen overtuigend bewijs voor EN het zegt helemaal niks over worp 1001
OPGELET bovenstaande tekst kan sporen van ironie en/of sarcasme bevatten
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
64bits - Core i3 - Acer A9Q1KNT - SPIN SP314-51 - Windows 11 Home - Firefox - Wifi - Telenet
-
Dicksy - Lid geworden op: 11 jul 2019, 20:17
Ik denk dat uw denkwijze verkeerd is en waarom:
De keuze voor doos C (A of B) is door toedoen van de quizmaster geëlimineerd en toch blijft u de keuzemogelijkheden behouden op 3 dozen.Wil. 08 aug 2023, 00:01
Een kwiskandidaat is bij het allerlaatste probleem gekomen dat hij moet oplossen. De situatie is deze:
De kandidaat staat voor een tafel waarop 3 dozen (A, B, C) geplaatst zijn. In 1 van deze dozen zit de autosleutel van een prachtige nieuwe wagen. Hij mag één keer kiezen.
Hij kiest doos A maar alvorens die doos te openen, doet de kwismaster, die goed weet in welke doos de sleutel zit, iets speciaals: hij opent doos C en laat zien dat er niets in die doos zit. Ze is leeg.
En nu stelt hij aan de kwiskandidaat de vraag of hij bij zijn keuze A blijft, want hij mag nu nog van gedacht veranderen aangezien doos A is toch nog niet geopend, en voor doos B kiezen. De kandidaat weet niet of de eerste doos de sleutel van die prachtige auto bevat. Hij weet nu enkel dat de sleutel niet in doos C zit.
Met zijn vraagstelling of hij bij zijn keuze blijft of nog wil veranderen doet hier niks meer ter zake maar dient enkel ter beïnvloeding, de sleutel zit misschien wel degelijk in doos A, de keuze van de kandidaat.
Als de kandidaat op voorhand doos A als keuze opgeeft en de quizmaster deze opent, goed wetende dat hij leeg is, verandert er voor de kandidaat niets, hij moet een keuze maken uit 2 dozen en niet uit 3.
-
Wil. - Lid geworden op: 15 nov 2005, 19:41
ET,
1. ik heb herhaaldelijk geschreven dat de quizmaster altijd een lege doos kiest uit de overgebleven groep.
Zoals hier: " De kwismaster toont dan één van de twee andere dozen en meer bepaald een lege."
en ook hier:
"Wanneer de gastheer van de show dan één doos ‘uitschakelt’ door een lege doos te openen – veronderstel C - "
en ook hier: "zodat degene die de erwt onder de beker gestopt heeft ook één lege beker van de twee overgebleven bekers kan omdraaien."
en ook nog hier: "dan zal de quizmaster één van de overgebleven dozen [A+B] openen en meer bepaald een lege"
2. hier staan alle mogelijke uitkomsten. Ik heb ook geschreven dat we ervan uitgaan dat de kandidaat doos A kiest maar dat het resultaat niet beïnvloed wordt als hij doos B of doos C kiest. De mogelijkheden blijven gelijkaardig: altijd wordt de kans vergroot tot 2 op 3 als je wisselt.
3. Statistiek betekent dat men een benaderende zekerheid geeft omtrent een uitkomst. Bij 1000 worpen met een munt, krijg je bij benadering 50% munt en 50% kruis; nooit 10% en 90%.
Dat is één van de grondslagen van statistiek.
Over worp 1001 zegt dat inderdaad niets, maar dat kwam in heel dit verhaal ook nergens aan de orde.
1. ik heb herhaaldelijk geschreven dat de quizmaster altijd een lege doos kiest uit de overgebleven groep.
Zoals hier: " De kwismaster toont dan één van de twee andere dozen en meer bepaald een lege."
en ook hier:
"Wanneer de gastheer van de show dan één doos ‘uitschakelt’ door een lege doos te openen – veronderstel C - "
en ook hier: "zodat degene die de erwt onder de beker gestopt heeft ook één lege beker van de twee overgebleven bekers kan omdraaien."
en ook nog hier: "dan zal de quizmaster één van de overgebleven dozen [A+B] openen en meer bepaald een lege"
2. hier staan alle mogelijke uitkomsten. Ik heb ook geschreven dat we ervan uitgaan dat de kandidaat doos A kiest maar dat het resultaat niet beïnvloed wordt als hij doos B of doos C kiest. De mogelijkheden blijven gelijkaardig: altijd wordt de kans vergroot tot 2 op 3 als je wisselt.
3. Statistiek betekent dat men een benaderende zekerheid geeft omtrent een uitkomst. Bij 1000 worpen met een munt, krijg je bij benadering 50% munt en 50% kruis; nooit 10% en 90%.
Dat is één van de grondslagen van statistiek.
Over worp 1001 zegt dat inderdaad niets, maar dat kwam in heel dit verhaal ook nergens aan de orde.
-
Wil. - Lid geworden op: 15 nov 2005, 19:41
Neen. Je gebruikt de verkeerde woorden en dat wijst erop dat je nog steeds vasthoudt aan je oorspronkelijk intuïtief aanvoelen.
Ik blijf niet de keuze behouden op 3 dozen maar wel op 2/3 van de kansen. Dat is iets anders.
Die vraagstelling is van groot belang: ze laat toe dat de kandidaat zijn kansen vergroot van 1 op 3 naar 2 op 3: een verdubbeling. Dat komt in de logische tabel ook tot uiting. Die logische tabel geeft alle mogelijkheden weer die zich kunnen voordoen een laat zien wat het resultaat is bij wisselen of bij vasthouden aan de keuze.Met zijn vraagstelling of hij bij zijn keuze blijft of nog wil veranderen doet hier niks meer ter zake maar dient enkel ter beïnvloeding, de sleutel zit misschien wel degelijk in doos A, de keuze van de kandidaat.
Onmogelijk. De gastheer opent nooit de keuze van de kandidaat. Dat is in het vertrek van deze discussie zo gegeven en dat is ook meerdere keren herhaald. Hij opent altijd één van de twee overige dozen en dat zal altijd een lege doos zijn.Als de kandidaat op voorhand doos A als keuze opgeeft en de quizmaster deze opent,