Wiskundig probleem

[Dicksy]

Net als ET ook deze posting niet gelezen, Dicksy?

Om hun theorie te staven blijft men de basis gebruiken die er aanvankelijk was, 3 dozen (3 x 33,33% kans).
De situatie is echter verandert door 1 doos te elimineren, 33,33% is verdwenen, dus gewoon weg.
Men heeft hierdoor een nieuwe situatie gecreëerd met een 2 x 50%-kans, wisselen of niet het blijft een 2 x50%-situatie.
Het is een theoretische benadering wat men hier doet.

[E.T.]

Wat doet dit stukje over gokken bij exacte wetenschappen

Wanneer ik je een probleem voorschotel in dit deel van het forum, dan vraag ik niet om er zomaar iets op te antwoorden. Ik wil dan een logisch-wetenschappelijk verklaring lezen. Die mis ik bij jouw uitleg.

Mijn uitleg is correct, weliswaar kort maar wel to-the-point en dat kan je van je gebazel met "logische" tabellen echt niet zeggen.

Ik ga nu stoppen maar ik weet wel wat te doen moest ik autosleutels in een doos kunnen winnen, waarvoor mijn dank Wil,

[Wil.]

Net als ET ook deze posting niet gelezen, Dicksy?

Om hun theorie te staven blijft men de basis gebruiken die er aanvankelijk was, 3 dozen (3 x 33,33% kans).
De situatie is echter verandert door 1 doos te elimineren, 33,33% is verdwenen, dus gewoon weg.
Men heeft hierdoor een nieuwe situatie gecreëerd met een 2 x 50%-kans, wisselen of niet het blijft een 2 x50%-situatie.
Het is een theoretische benadering wat men hier doet.

De eerste vraag die ik je stel is: is die theoretische benadering correct?

[Wil.]

Wat doet dit stukje over gokken bij exacte wetenschappen

Omdat het gaat over statistiek en - geloof me - dat is héél zeker gebaseerd op de exacte wetenschappen, nl. wiskunde.

Wanneer ik je een probleem voorschotel in dit deel van het forum, dan vraag ik niet om er zomaar iets op te antwoorden. Ik wil dan een logisch-wetenschappelijk verklaring lezen. Die mis ik bij jouw uitleg.

Mijn uitleg is correct, weliswaar kort maar wel to-the-point en dat kan je van je gebazel met "logische" tabellen echt niet zeggen.

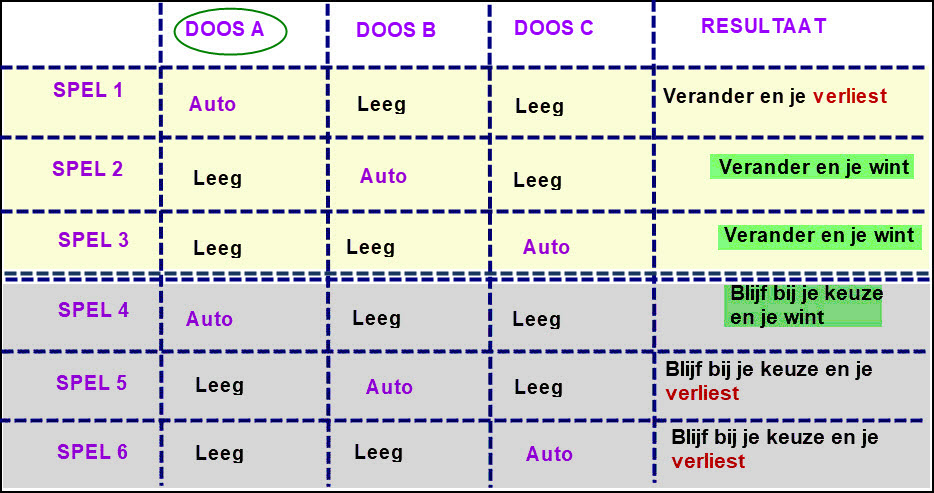
Hij is kort, dat wel, maar fout. De logische tabel op blz. 8 - indien je die begrijpt ??? -- ik vrees van niet - wijst je daarop. Alle mogelijkheden staan daar en de uitkomst ook.


E.T. uit je vraagstelling en je reacties kom ik tot de bevinding dat jij dit probleem niet kunt vatten. Het gaat je denkvermogen te boven. Ik verwacht me eraan dat je daarom ook steeds dezelfde foute denkwijze gaat blijven herhalen.

Dat is niet verwonderlijk wanneer men heeft vastgesteld dat zelfs sommigen van de meest bekende proffen hier in eerste instantie in de val van het intuïtief denken zijn gelopen.

[E.T.]

De vraag die ik jullie stel is om in heel gewone taal uit te leggen waarom hij meer kans maakt op het winnen van de prijs door niet bij zijn oorspronkelijke keuze te blijven maar te veranderen ...

We zullen het verhaaltje tot de essentie herleiden:
Drie dozen waarvan twee leeg en in vol (met gebakken lucht)
Je kiest er één de andere twee gaan naar de andere kant
jij dus 1 doos tegenover 2 dozen voor rechts
kans om te winnen 1/3 tegen 2/3
of (speciaal voor Wil,) in percenten
links 33,3 tegen 66,6 rechts

als je de kans krijgt om te wisselen zou je wel goed gek zijn om het niet te doen

[Wil.]

Dat was een nachtelijke poging, merk ik.
De beschrijving is nochtans incorrect omdat een essentieel punt niet vermeld staat. Wat ik al suggereerde: het gaat jou niet lukken.

[Dicksy]

Om hun theorie te staven blijft men de basis gebruiken die er aanvankelijk was, 3 dozen (3 x 33,33% kans).
De situatie is echter verandert door 1 doos te elimineren, 33,33% is verdwenen, dus gewoon weg.
Men heeft hierdoor een nieuwe situatie gecreëerd met een 2 x 50%-kans, wisselen of niet het blijft een 2 x50%-situatie.
Het is een theoretische benadering wat men hier doet.

Heeft men nu 2 dozen met elk 33,33% kans op de sleutel? Nee, men heeft nu 2 dozen met elk 50% kans om die doos met de sleutel te kiezen en geen 66,66% kans dat men juist kiest.

[Wil.]

Om hun theorie te staven blijft men de basis gebruiken die er aanvankelijk was, 3 dozen (3 x 33,33% kans).
De situatie is echter verandert door 1 doos te elimineren, 33,33% is verdwenen, dus gewoon weg.
Men heeft hierdoor een nieuwe situatie gecreëerd met een 2 x 50%-kans, wisselen of niet het blijft een 2 x50%-situatie.
Het is een theoretische benadering wat men hier doet.

Heeft men nu 2 dozen met elk 33,33% kans op de sleutel? Nee, men heeft nu 2 dozen met elk 50% kans om die doos met de sleutel te kiezen en geen 66,66% kans dat men juist kiest.

Is dat een antwoord op mijn vraag 'is die theoretische benadering correct?' ? Indien je antwoord 'neen' is, dan moet de logische tabel dat duidelijk maken. De kansen moeten dan volgens de tabel 50/50 zijn.
Dat is niet het geval en elke universitaire paper over die zaak bevestigt dat.

Misschien is er in de tabel een mogelijkheid over het hoofd gezien en misschien zijn er wel 4 mogelijkheden waar de sleutel zich kan bevinden, maar volgens mij is dat niet zo. Dus ...

Wanneer je één enkel spel speelt, dan kan blijken dat de sleutel in je eerst gekozen doos zat en dat de andere doos leeg was. Als je het spel vele keren speelt, dan valt alles in zijn juiste plooi: de kansen gaan richting 1/3 vs 2/3 en dat is ook de mate waarin je je kans kunt vergroten.

[Dicksy]

Wil. 08 aug 2023, 00:01

Hij kiest doos A maar alvorens die doos te openen, doet de kwismaster, die goed weet in welke doos de sleutel zit, iets speciaals: hij opent doos C en laat zien dat er niets in die doos zit. Ze is leeg.
En nu stelt hij aan de kwiskandidaat de vraag of hij bij zijn keuze A blijft, want hij mag nu nog van gedacht veranderen aangezien doos A is toch nog niet geopend, en voor doos B kiezen. De kandidaat weet niet of de eerste doos de sleutel van die prachtige auto bevat. Hij weet nu enkel dat de sleutel niet in doos C zit.

Heeft hij er voordeel bij om zijn keuze A te veranderen in keuze B of niet? Ik ga het antwoord al verklappen. Ja, hij heeft meer kans om de prijs te winnen indien hij verandert van mening en voor doos B kiest.

Dicksy 39 minuten geleden

Om hun theorie te staven blijft men de basis gebruiken die er aanvankelijk was, 3 dozen (3 x 33,33% kans).
De situatie is echter verandert door 1 doos te elimineren, 33,33% is verdwenen, dus gewoon weg.

Heeft men nu 2 dozen met elk 33,33% kans op de sleutel? Nee, men heeft nu 2 dozen met elk 50% kans om die doos met de sleutel te kiezen en geen 66,66% kans dat men juist kiest.

Of 1 kans van 66,66% om die auto te winnen. Nee, het blijft 50% kans op winst en 50% kans op verlies.

Meer woorden maak ik er nu echt niet meer aan vuil.

[E.T.]

Dat was een nachtelijke poging, merk ik.
De beschrijving is nochtans incorrect omdat een essentieel punt niet vermeld staat. Wat ik al suggereerde: het gaat jou niet lukken.

Ik kan maar blijven proberen hé maar voor mij is het zo duidelijk zonder al de woordenkramerij.

Eens je keuze gemaakt liggen de kansen VAST.

Je start altijd met een achterstand van 1/3 tegen 2/3

[Wil.]

Nee, men heeft nu 2 dozen met elk 50% kans om die doos met de sleutel te kiezen en geen 66,66% kans dat men juist kiest.

Dan moet er wel een fout in de logische tabel zitten. Die aanwijzen blijkt onmogelijk.

De wetenschappelijke wereld is het erover eens dat het 66% is.

Het experiment toont aan hoe diep doordringend het intuïtief denken is terwijl het ondergeschikt zou moeten zijn aan het logisch denken.
In dit boek worden dergelijke verkeerde denkwijzen ontleed:



Over dit 3-dozen probleem lees je:

"No other statistical puzzle comes close to fooling all the people all the time" -- daaruit blijkt dat het wellicht het moeilijkst te aanvaarden denkprobleem van die aard is. Zelfs als de weg naar de oplossing getoond wordt, weigert de intuïtieve geest om de logica te aanvaarden. Raar.

[E.T.]

@Dicksy
De kansen op de juiste doos zijn van in het begin 33,3 tegen 66,6
Het openen van doos veranderd daar just niks aan ...
de sleutel zit waar hij zit

[Dicksy]

door E.T. » 41 minuten geleden
@Dicksy
De kansen op de juiste doos zijn van in het begin 33,3 tegen 66,6
Het openen van doos veranderd daar just niks aan ...
de sleutel zit waar hij zit.

Van in het begin, daar heb ik geen probleem mee bij die 3 dozen. Voor mij verandert het de zaak vanaf het moment dat men die ene doos elimineert.
50% dat de sleutel in doos A zit en 50% dat de sleutel in doos B zit. Ik houd geen rekening meer met de kansen die er bestonden bij 3 dozen (33% tegen 66%) gewoon omdat doos C niet meer meespeelt. En de sleutel zit inderdaad waar hij zit....50% kans in A en 50% kans in B.
Het zal wel aan mij liggen, dus case closed voor mij.

[E.T.]

No other statistical puzzle comes close to fooling all the people all the time"

Foei Wil, en dat laat je los op ons arme senioren

[Wil.]

Nog een bijkomend punt:

Wanneer iemand meent dat de kans 50/50 is op winst, dan gaat de overgrote meerderheid van deze mensen niet veranderen maar bij hun eerste keuze blijven.
Wat is daarvoor de reden? Daniel Kahneman - nobelprijs economie 2002 en specialist in beslissingstheorie - heeft onderzoek gedaan naar de 'pijnervaring' bij verlies. Het blijkt dat de proefpersonen veel langer de pijn (psychologische of financiële pijn) bij verlies blijven onthouden dan het plezier van te winnen.

Wanneer iemand denkt dat hij in de situatie van de 3-dozenpuzzel 50% kans heeft en hij wisselt toch, dan is de kans volgens hem voor 50% aanwezig dat hij een lege doos kiest en dat zijn eigen eerste keuze dus de juiste was. Dan zou door die wissel een 'pijn' ontstaan die had kunnen vermeden worden door gewoon niet te veranderen. En áls die eerste keuze tóch een lege doos zou blijken te zijn, dan kan men dat in elk geval niet wijten aan een verkeerde actie; dan was 'het lot' verantwoordelijk want het was zogezegd 50/50 .
En dus wisselt de meerderheid van de spelers niet.