Wiskundige problemen en probleempjes 2

denook · 06 okt 2009, 20:58

dinsdag 6 oktober 2009

tien problemen en proleempjes

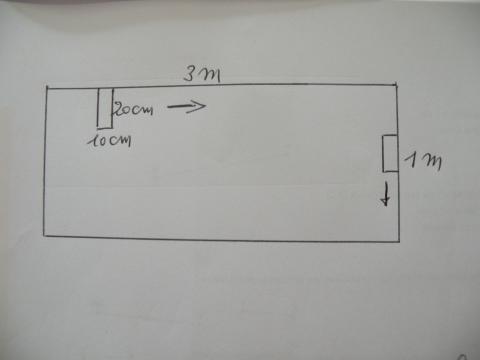
1) Een leraar veegt een rechthoekig bord van 3 meter bij 1 meter
met een rechthoekige spons van 20 cm bij 10 cm. Hij volgt daarbij
de rand zoals op de figuur aangeduid zonder de spons te draaien.
Welke oppervlakte is na één rondje schoon geveegd?

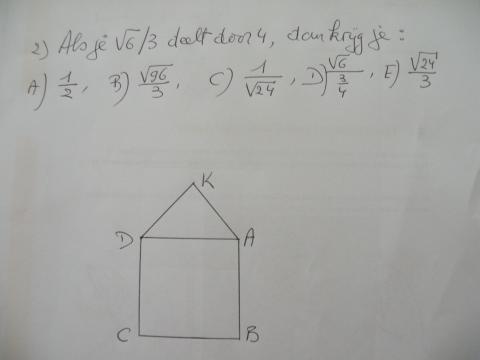
Afbeelding

3) zie tekening hierboven
Als het vierkant ABCD een omtrek heeft van 32 cm en de driehoek
DAK een omtrek van 18 cm, wat is dan de omtrek van de
vijfhoek ABCDK?

4) Schrijf als een breuk: 2,31646464...

5) Op een weegschaal houden elkaar in evenwicht:
1 glas + 1 plant - tegenover - 1 kat,
1 glas + 1 fles - tegenover - 1 plant
2 katten - tegenover - 3 flessen
vul aan
1 plant - tegenover - ??? glazen

6) Je hebt vijf stukken ketting, elk bestaande uit drie schakels.
Je wilt één lange, niet gesloten ketting maken uit deze vijf stukken.
Een schakel openbreken kost 1 euro en een schakel weer sluiten
kost 3 euro. Wat is de laagste prijs om één lange, niet gesloten
ketting te maken?

7) Voor hoeveel natuurlijke getallen n is 2009:n ook een natuurlijk
getal?

8 ) Drie leerlingen doen een uitspraak over een driehoek.
Kwik: de driehoek is rechthoekig en gelijkzijdig,
Kwek: de driehoek is stomphoekig en gelijkzijdig,
Kwak: de driehoek is rechthoekig en gelijkbenig.
Wie deed een foute uitspraak?

9) In een zeshoek zijn twee overstaande hoeken recht.
De andere vier hoeken zijn gelijk aan elkaar.
Als elke zijde 1 m is, wat is dan de oppervlakte van de zeshoek?
(- sloeberkebebo mag altijd een passende figuur meegeven-)

10) Als p1, p2, p3, p4 en p5 de vijf kleinste priemgetallen zijn, in een
WILLEKEURIGE volgorde, en
n = p1.p2 + p3.p4.p5,
welke van volgende uitspraken is dan juist?
A) n is even,
B) n is een priemgetal,
C) n is kleiner dan 300,
D) n is groter dan 100,
E) n is niet deelbaar door een priemgetal kleiner dan 12.
nog eens: let op, p1 ... tot p5 staan in een willekeurige volgorde!!

veel succes iedereen;
voor nieuwe medespelers - steeds welkom -
eerst wel lezen blz 1.

goede avond,
denook

lotte · 06 okt 2009, 21:22

Beste allen,

4) Schrijf als een breuk: 2,31646464...

22933/9900

goeie avond
lotte.

sloeberkebebo · 06 okt 2009, 23:00

Goeden avond allemaal

Vraag 9

In een zeshoek zijn twee overstaande hoeken recht.
De andere vier hoeken zijn gelijk aan elkaar.
Als elke zijde 1 m is, wat is dan de oppervlakte van de zeshoek?
(- sloeberkebebo mag altijd een passende figuur meegeven-)

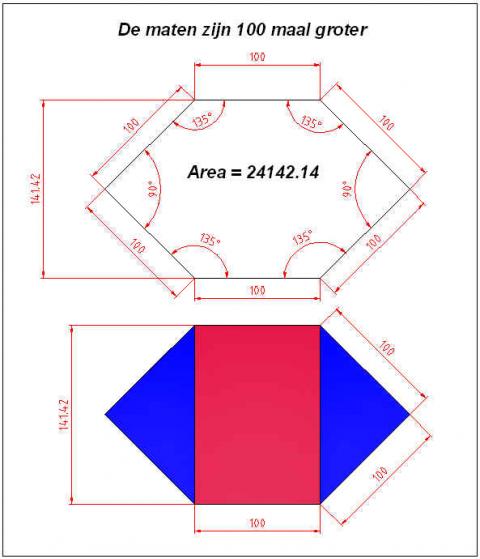
De opp. = 2.41... m²

Tek. volgt

Groetjes

Sloeber

troontje · 06 okt 2009, 23:04

goede avond allen

vraag5

0,25(glas)--1,25(plant)=1,50(kat)
0,25(glas)--1(fles)=1,25(plant)
3(2 katten)=1x3(flessen)=3
1,25(plant)=5x0,25(glazen)=1,25

troontje,

sloeberkebebo · 06 okt 2009, 23:42

Vraag 9

mvg

Sloeber

oomski · 06 okt 2009, 23:48

Goedenavond iedereen.
Vraag 1:

lange zijden elk 30 sponzen en de korte zijden elk 3 sponzen
Samen 66 sponzen van 20x10= 200x66 = 13200cm²

pastoor · 07 okt 2009, 08:13

Goede morgen allemaal.

Troontje: 1,25(plant)=5x0,25(glazen)=1,25
Dat is juist.

Of 1 plant is op de weegschaal in evenwicht met 5 glazen. (duidelijker?)

pastoor · 07 okt 2009, 08:26

Vraag 2.

B: (vierkantwortel(6))/(3/4) = (vierkantwortel(6))(4)/(3) =
(vierkantwortel(96))/(3)

D: (vierkantwortel(6))/(3) gedeeld door 4 is(vierkantwortel(6))/(3/4)

Zowel B als D zijn juiste oplossingen.

denook · 07 okt 2009, 19:21

... een dag later ...

alle leerlingen (-steeds dezelfde vijf -) losten een oefening op;
met succes, want viermaal juist.
Het moest eigenlijk vijf maal juist zijn; lees maar verder - verrassing...

vraag 4) lotte - ok
goed de les van vorige week gevolgd,
want daar kwam de oefening uit

vraag 9) sloeverkebebo - ok
uitleg bij zijn figuur:
elke blauwe driehoek heeft basis en hoogte van 1 meter,
dus met oppervlakte (1 . 1)/2 = 1/2
de twee driehoeken: 2 . 1/2 = 1
de blauwe rechthoek heeft als basis 1 meter
en de hoogte is de schuine zijde van de rechthoekige driehoek;
met Pythagoras: vierkantswortel uit (1² + 1²) = wortel2
oppervlakte rechthoek: 1 . wortel2 = wortel2
totale oppervlakte:
1 meter² + (wortel2) meter² = (1 + wortel2)vierkante meter
= 2,41421356237...

vraag 5) troontje - ok ...
maar wat is dat allemaal - typisch troontjes wiskunde;
toch juist: 1 plant - tegenover - 5 glazen

vraag 1) oomski - ok
kort, krachtig en juist

vraag 2) pastoor - ... niet juist ...
wie had dat gedacht: alle leerlingen juist, alleen onze beste leerling
laat een steekje vallen.
Was het gisteravond te laat geworden - was hij nog wat slaperig -
een ogenblik verstrooid?
We weten het niet.
We weten allemaal, ook pastoor uiteraard, dat,
als je iets positief DEELT door vier, je dan iets KLEINER krijgt.
De antwoorden B en D geven een groter getal na deling door vier

tot hier

blijven over: 3 / 6 / 7 / 8 / 10 en 2.
op vraag 2 moet NIET gewacht worden tot na je 24 uur;
het is immers een verbetering van het antwoordd van een medeleerling

tot morgen,
denook

pastoor · 07 okt 2009, 19:27

Antwoord op vraag 2 is C, of 1/ (vierkantswortel van 24).

((√6)/3)/4 = (√6)/12 = (√3.√2)/(√3√3√2√2√2√2) = 1/(√3√2√2√2) = 1/√24

lotte · 07 okt 2009, 21:27

Beste denook, beste allen

6) Je hebt vijf stukken ketting, elk bestaande uit drie schakels.
Je wilt één lange, niet gesloten ketting maken uit deze vijf stukken.
Een schakel openbreken kost 1 euro en een schakel weer sluiten
kost 3 euro. Wat is de laagste prijs om één lange, niet gesloten
ketting te maken?

van l ketting de 3 schakels openen --- 3*1€
andere 4 kettingen aan één maken met de 3 geopende schakels --- 3*3€

open ketting kost minimaal 12€ ?

goeie avond
lotte.

sloeberkebebo · 07 okt 2009, 23:00

Goeden avond allemaal ,

Vraag 3 zie tekening hieronder
Als het vierkant ABCD een omtrek heeft van 32 cm en de driehoek
DAK een omtrek van 18 cm, wat is dan de omtrek van de
vijfhoek ABCDK?

De omtrek van de vijfhoek ABCDK = 34 cm

Afbeelding

Groetjes

Sloeber

troontje · 07 okt 2009, 23:15

goeie avond.

vraag 8

De foute uitspraak is van Kwik: de driehoek is rechthoekig en gelijkzijdig

slaapwel allen,
troontje

sloeberkebebo · 08 okt 2009, 08:49

Beste Troontje

Ik ben het niet eens met uw antwoord .

8 ) Drie leerlingen doen een uitspraak over een driehoek.
Kwik: de driehoek is rechthoekig en gelijkzijdig,
Kwek: de driehoek is stomphoekig en gelijkzijdig,
Kwak: de driehoek is rechthoekig en gelijkbenig. =====> O.K.
Wie deed een foute uitspraak?

Kwik en Kwek zijn fout !

Afbeelding

### Van een gelijkzijdige driehoek zijn alle hoeken ( 60° ) en zijden gelijk .

pastoor · 08 okt 2009, 13:13

Goede dag allemaal.

vraag 10) Als p1, p2, p3, p4 en p5 de vijf kleinste priemgetallen zijn, in een WILLEKEURIGE volgorde, en n = p1.p2 + p3.p4.p5,
welke van volgende uitspraken is dan juist?
A) n is even,
B) n is een priemgetal,
C) n is kleiner dan 300,
D) n is groter dan 100,
E) n is niet deelbaar door een priemgetal kleiner dan 12.
nog eens: let op, p1 ... tot p5 staan in een willekeurige volgorde!

De priemgetallen zijn 2, 3, 5, 7, en 11.
[color=red]Antwoord, alleen E is juist.[/color]