Wiskundige problemen en probleempjes 2
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste Ad Fundum,
in het vijfde Middelbaar zijn er afdelingen met 3, 4, 6 of 8 uren
wiskunde per week.
In een school op niveau zullen de leerlingen van de 6- en 8-uur
met een dergelijke opgave spelen.
Ze stellen de onbekenden daar voor door x, y, z, u en v.
Dan schrijven ze de vergelijkingen mooi onder elkaar en vermits
er hier in elke vergelijking onbekenden ontbreken lossen ze deze
zeer vlug op - wiskundig.
De logische oplossing - zoals pastoor het deed - gaat hier ook,
juist omdat het zo'n eenvoudige vergelijkingen zijn.
Moesten in de 5 vergelijkingen alle 5 de onbekenden voorkomen,
dan kan het alleen maar wiskundig en niet meer door logisch denken.
Tot daar.
Vermits je op onze topic kwam met je probleem neem ik aan dat je
af en toe ook eens komt lezen. Zo zijn er velen, doch weinigen spelen
mee.
Word jij een nieuwe leerling ?
Onze topic is ook niet de plaats waar we de huistaken van de leerlingen
uit de humaniora willen oplossen - dat begrijp je hopelijk ook wel.
groetjes,
denook
in het vijfde Middelbaar zijn er afdelingen met 3, 4, 6 of 8 uren
wiskunde per week.
In een school op niveau zullen de leerlingen van de 6- en 8-uur
met een dergelijke opgave spelen.
Ze stellen de onbekenden daar voor door x, y, z, u en v.
Dan schrijven ze de vergelijkingen mooi onder elkaar en vermits
er hier in elke vergelijking onbekenden ontbreken lossen ze deze
zeer vlug op - wiskundig.
De logische oplossing - zoals pastoor het deed - gaat hier ook,
juist omdat het zo'n eenvoudige vergelijkingen zijn.
Moesten in de 5 vergelijkingen alle 5 de onbekenden voorkomen,
dan kan het alleen maar wiskundig en niet meer door logisch denken.
Tot daar.
Vermits je op onze topic kwam met je probleem neem ik aan dat je
af en toe ook eens komt lezen. Zo zijn er velen, doch weinigen spelen
mee.
Word jij een nieuwe leerling ?
Onze topic is ook niet de plaats waar we de huistaken van de leerlingen
uit de humaniora willen oplossen - dat begrijp je hopelijk ook wel.
groetjes,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
Dinsdag 21 uur – wiskundetijd – problemen en probleempjes
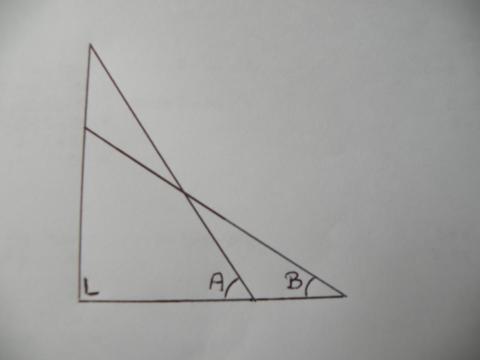
1) Twee congruente driehoeken worden op elkaar geplaatst, zoals in de figuur.
Als de hoek A gelijk is aan 57°33’, hoe groot is dan hoek B?
2)In een ballenbad liggen 30 000 ballen. 1% zijn blauwe ballen en 99% zijn rode ballen.
We halen er enkele rode ballen uit, tot er in het nieuwe totaal nog 97% rode ballen zijn.
Hoeveel rode ballen liggen er nu nog in het bad?
3) In een vierhoek ABCD zijn de hoeken B en D recht.
Verder meten de lijnstukken BC, CD en DA respectievelijk 1m, 4m en 3m.
Bereken de oppervlakte van de vierhoek ABCD. (sloeberkebebo mag tekening plaatsen).
4) Zeven kinderen van een huisgezin verjaren allen op dezelfde dag, met telkens één jaar verschil. De drie jongsten zijn samen 42 jaar oud. Hoe oud zijn de drie oudsten samen?
5) Een cilindervormige rechtstaande tank is ingegraven. Midden boven het bovenvlak is een spongat waardoor een peilstok kan gestoken worden. Als we de peilstok recht omlaag steken meten we 180 cm voor de hoogte en een oliepeil van 36 cm. Zetten we de peilstok helemaal schuin waar bodem en wand samenkomen, dan meten we voor het peil 39 cm. Hoeveel liter olie zit er nog in de tank?
6) Bereken de afstand tussen A en B in volgende figuur. A ligt in het midden van de straal van de cirkel en AB is diagonaal van een rechthoek waarvan één hoekpunt op de cirkel ligt.
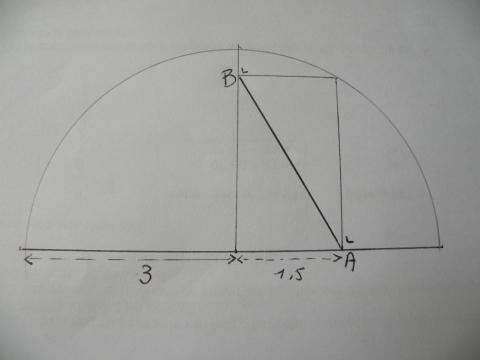
7) Hoeveel punten kunnen een cirkel en een rechthoek gemeen hebben? – alle mogelijkheden geven –
8 ) Een bus vervoert 7 kinderen. Ieder kind heeft 7 rugzakken. In iedere rugzak zitten 7 katten. Iedere kat ontfermt zich over 7 kleine katjes.
Hoeveel benen en poten samen zijn er op de bus?
9) Men vormt een rij getallen met als eerste term 4² en als tweede term 2-tot de macht4. De derde term is het quotiënt van de eerste en de tweede term. De vierde term is het quotiënt van de tweede en de derde term; en zo verder. Als we de tien eerste termen van de rij met elkaar vermenigvuldigen, waaraan is het product dan gelijk?
10) Ik zet achteraan een getal een ‘nul’ bij. Zo wordt het oorspronkelijke getal vermeerderd met 1107. Wat was het oorspronkelijke getal?
Veel succes iedereen –
nieuwe leerlingen lezen eerst blz 1.
Tot morgen - denook
1) Twee congruente driehoeken worden op elkaar geplaatst, zoals in de figuur.
Als de hoek A gelijk is aan 57°33’, hoe groot is dan hoek B?

2)In een ballenbad liggen 30 000 ballen. 1% zijn blauwe ballen en 99% zijn rode ballen.
We halen er enkele rode ballen uit, tot er in het nieuwe totaal nog 97% rode ballen zijn.
Hoeveel rode ballen liggen er nu nog in het bad?
3) In een vierhoek ABCD zijn de hoeken B en D recht.
Verder meten de lijnstukken BC, CD en DA respectievelijk 1m, 4m en 3m.
Bereken de oppervlakte van de vierhoek ABCD. (sloeberkebebo mag tekening plaatsen).
4) Zeven kinderen van een huisgezin verjaren allen op dezelfde dag, met telkens één jaar verschil. De drie jongsten zijn samen 42 jaar oud. Hoe oud zijn de drie oudsten samen?
5) Een cilindervormige rechtstaande tank is ingegraven. Midden boven het bovenvlak is een spongat waardoor een peilstok kan gestoken worden. Als we de peilstok recht omlaag steken meten we 180 cm voor de hoogte en een oliepeil van 36 cm. Zetten we de peilstok helemaal schuin waar bodem en wand samenkomen, dan meten we voor het peil 39 cm. Hoeveel liter olie zit er nog in de tank?
6) Bereken de afstand tussen A en B in volgende figuur. A ligt in het midden van de straal van de cirkel en AB is diagonaal van een rechthoek waarvan één hoekpunt op de cirkel ligt.

7) Hoeveel punten kunnen een cirkel en een rechthoek gemeen hebben? – alle mogelijkheden geven –
8 ) Een bus vervoert 7 kinderen. Ieder kind heeft 7 rugzakken. In iedere rugzak zitten 7 katten. Iedere kat ontfermt zich over 7 kleine katjes.
Hoeveel benen en poten samen zijn er op de bus?
9) Men vormt een rij getallen met als eerste term 4² en als tweede term 2-tot de macht4. De derde term is het quotiënt van de eerste en de tweede term. De vierde term is het quotiënt van de tweede en de derde term; en zo verder. Als we de tien eerste termen van de rij met elkaar vermenigvuldigen, waaraan is het product dan gelijk?
10) Ik zet achteraan een getal een ‘nul’ bij. Zo wordt het oorspronkelijke getal vermeerderd met 1107. Wat was het oorspronkelijke getal?
Veel succes iedereen –
nieuwe leerlingen lezen eerst blz 1.
Tot morgen - denook
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
Goeie avond denook en alle medeleerlingen
Vraag 8
Een bus vervoert 7 kinderen. Ieder kind heeft 7 rugzakken. In iedere rugzak zitten 7 katten. Iedere kat ontfermt zich over 7 kleine katjes.
Hoeveel benen en poten samen zijn er op de bus?
(7 kinderen * 7 rugzakken) * (7*8 poezen/katjes) * 4 poten
7 kinderen * 2 benen
(49*56*4) + 14
10.990 pootjes en benen
als die in de bus is
+ 1 buschauffeur * 2 benen
groetjes
lotte.
Vraag 8
Een bus vervoert 7 kinderen. Ieder kind heeft 7 rugzakken. In iedere rugzak zitten 7 katten. Iedere kat ontfermt zich over 7 kleine katjes.
Hoeveel benen en poten samen zijn er op de bus?
(7 kinderen * 7 rugzakken) * (7*8 poezen/katjes) * 4 poten
7 kinderen * 2 benen
(49*56*4) + 14
10.990 pootjes en benen
als die in de bus is
+ 1 buschauffeur * 2 benen
groetjes
lotte.
Laatst gewijzigd door lotte op 10 nov 2009, 21:08, 1 keer totaal gewijzigd.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Vraag 6
Bereken de afstand tussen A en B in volgende figuur. A ligt in het midden van de straal van de cirkel en AB is diagonaal van een rechthoek waarvan één hoekpunt op de cirkel ligt.

mvg
Sloeber
Bereken de afstand tussen A en B in volgende figuur. A ligt in het midden van de straal van de cirkel en AB is diagonaal van een rechthoek waarvan één hoekpunt op de cirkel ligt.

mvg
Sloeber
Meten is weten - Carpe diem
-
oomski - Lid geworden op: 28 mei 2008, 08:25
- Locatie: Thuis.
Goedenacht iedereen.
Vraag 4:
De drie jongesten zijn samen 42 jaar
Dus de jongste is 13, tweede jongste 14 en derde jongste 15
de drie oudsten zijn 17, 18 en 19 jaar dus samen 54 jaar.
Bij vraag 2, (wat mijn eerste probeersel was ), kwam ik ook op 10000 ballen in totaal, 300 blauwe en 9700 rode.
), kwam ik ook op 10000 ballen in totaal, 300 blauwe en 9700 rode.
Vraag 4:
De drie jongesten zijn samen 42 jaar
Dus de jongste is 13, tweede jongste 14 en derde jongste 15
de drie oudsten zijn 17, 18 en 19 jaar dus samen 54 jaar.
Bij vraag 2, (wat mijn eerste probeersel was
Wie op wraak zint, houdt zijn eigen wonden open.
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
Pastoor,pastoor schreef:Goede avond allemaal.
Vraag 2: Er zijn nog 9700 rode ballen in het ballenbad.
mag proberen aan te vullen
met hetzelfde resultaat als oplossing
1% van de ballen is blauw= 300 ballen
99% is rood = 29.700 ballen
Wanneer je nu rode ballen verwijdert is de 97 % die overblijft, 97% van een aantal ballen dat we niet kennen
dus niet meer van de 30.000
300 blauwe ballen over dat is nu 3%
1% van de resterende ballen = 97
voor zij die sint-maarten vieren
een fijne dag samen
groetjes
lotte