Wiskundige problemen en probleempjes 2
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste Troontje ,
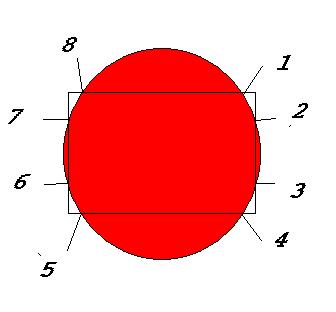
Alles eens rustig nazien .....over vraag 5 ( zie ook mijn figuurtje ..... )
1dm³ = 1 liter
Wij moeten het volume zoeken van de schijf in dm³ .
Dat is de oppervlakte van het grondvlak maal de schijfhoogte .
Daarvoor moeten wij eerst de diameter van de cilinder kennen .
Die kunnen wij vinden met de maten 36 cm en 39 cm zoals beschreven .
Met 36 cm rechthoekszijde en 39 cm schuine zijde en met de stelling van Pythagoras berekenen wij de korte zijde ( 15 cm ) van deze driehoek en wij nemen nu ( 180 cm / 36 cm = 5 ) maal deze maat en wij hebben de straal van onze cilinderschijf ( 15 cm * 5 = 75 cm ).Opgepast alle maten zijn in cm ............
Vele groetjes en leesgenot Sloeber
Alles eens rustig nazien .....over vraag 5 ( zie ook mijn figuurtje ..... )
1dm³ = 1 liter
Wij moeten het volume zoeken van de schijf in dm³ .
Dat is de oppervlakte van het grondvlak maal de schijfhoogte .
Daarvoor moeten wij eerst de diameter van de cilinder kennen .
Die kunnen wij vinden met de maten 36 cm en 39 cm zoals beschreven .
Met 36 cm rechthoekszijde en 39 cm schuine zijde en met de stelling van Pythagoras berekenen wij de korte zijde ( 15 cm ) van deze driehoek en wij nemen nu ( 180 cm / 36 cm = 5 ) maal deze maat en wij hebben de straal van onze cilinderschijf ( 15 cm * 5 = 75 cm ).Opgepast alle maten zijn in cm ............
Vele groetjes en leesgenot Sloeber
Meten is weten - Carpe diem
-
troontje - Lid geworden op: 14 dec 2004, 10:03
sorry Sloeberkebebo,ik had niet eens gezien dat vraag 5 opgelost was en dan nog met een duidelijke tekening van jou 

tja ,vraag gelezen en opgelost tussen de soep en de patatten,alé emmer en dweil
ik ga het maar verwijderen alvorens de meester het ziet,
ik dacht al, amai zo gemakkelijk niet dus
niet dus 
bedankt sloeberbeko voor de deskundige uitleg
troontje
tja ,vraag gelezen en opgelost tussen de soep en de patatten,alé emmer en dweil
ik ga het maar verwijderen alvorens de meester het ziet,
ik dacht al, amai zo gemakkelijk
bedankt sloeberbeko voor de deskundige uitleg
troontje
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
vervolg evaluatie:
vraag 10) - lotte - ok
het oorspronkelijke getal is wel degelijk 123;
met de 'nul' er achter wordt het 1230
vraag 9) - pastoor -ok
en met meer dan voldoende uitleg - mooi ook
vraag 5) - sloeberkebebo -ok - en hoe !!
prachtige figuur - juist berekend ook -
+ achteraf uitleg nog eens verfijnd naar troontje toe.
Wel sloeberkebebo: Pythagoras, gelijkvormige figuren,
formule inhoud van cilinder, overgang cm³ naar dm³ naar liter.
En dat voor iemand die beweert alleen te kunnen tekenen en meten ...
dit was ook in mijn ogen de moeilijkste opgave.
vraag 1) - oomski - bijna ok
je blijft óf in tientallig stelsel, óf je werkt met zestigdelige graden;
niet mengen. Zo is 15,50° = 15°30', wat je wel wist.
Ook hier was sloeberkebebo weer actief.
blijven over: vragen 3 en 7
tot morgen?
denook
oh ja, voor sloeberkebebo: in oefening 6 was inderdaad de diagonaal
gelijk aan de andere diagonaal, die dan weer de straal was en dus 3m.
Had (-verstrooid-) een nogal ingewikkelde formule in het hoofd - sorry
vervolg evaluatie:
vraag 10) - lotte - ok
het oorspronkelijke getal is wel degelijk 123;
met de 'nul' er achter wordt het 1230
vraag 9) - pastoor -ok
en met meer dan voldoende uitleg - mooi ook
vraag 5) - sloeberkebebo -ok - en hoe !!
prachtige figuur - juist berekend ook -
+ achteraf uitleg nog eens verfijnd naar troontje toe.
Wel sloeberkebebo: Pythagoras, gelijkvormige figuren,
formule inhoud van cilinder, overgang cm³ naar dm³ naar liter.
En dat voor iemand die beweert alleen te kunnen tekenen en meten ...
dit was ook in mijn ogen de moeilijkste opgave.
vraag 1) - oomski - bijna ok
je blijft óf in tientallig stelsel, óf je werkt met zestigdelige graden;
niet mengen. Zo is 15,50° = 15°30', wat je wel wist.
Ook hier was sloeberkebebo weer actief.
blijven over: vragen 3 en 7
tot morgen?
denook
oh ja, voor sloeberkebebo: in oefening 6 was inderdaad de diagonaal
gelijk aan de andere diagonaal, die dan weer de straal was en dus 3m.
Had (-verstrooid-) een nogal ingewikkelde formule in het hoofd - sorry
Laatst gewijzigd door denook op 12 nov 2009, 23:18, 1 keer totaal gewijzigd.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goeden avond allemaal ,
Vraag 3
In een vierhoek ABCD zijn de hoeken B en D recht.
Verder meten de lijnstukken BC, CD en DA respectievelijk 1m, 4m en 3m.
Bereken de oppervlakte van de vierhoek ABCD.
(3*4)/2=6 m² Opp A
(24^0.5 * 1 ) / 2 = 2,4495 m² Opp B
Opp A + Opp B = Opp vierhoek ABCD = 8,4495 m²

Groetjes
Sloeber
Vraag 3
In een vierhoek ABCD zijn de hoeken B en D recht.
Verder meten de lijnstukken BC, CD en DA respectievelijk 1m, 4m en 3m.
Bereken de oppervlakte van de vierhoek ABCD.
(3*4)/2=6 m² Opp A
(24^0.5 * 1 ) / 2 = 2,4495 m² Opp B
Opp A + Opp B = Opp vierhoek ABCD = 8,4495 m²

Groetjes
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Vraag 7) Hoeveel punten kunnen een cirkel en een rechthoek gemeen hebben? – alle mogelijkheden geven –
Aantal mogelijkheden: 0,1,2,3,4 of 5
Hiervan zijn er 1 of 2 of 3 of 4 mogelijke gemeenschappelijke punten.
Aantal mogelijkheden: 0,1,2,3,4 of 5
Hiervan zijn er 1 of 2 of 3 of 4 mogelijke gemeenschappelijke punten.
Sudoku, wijntjes proeven, genieten.
-
oomski - Lid geworden op: 28 mei 2008, 08:25
- Locatie: Thuis.
Yeahhh, Sloeberkebo, dat bekwam ik ook. Ik dacht dat ik constant iets verkeerd deed omdat ik met een vierkantswortel zat, maar blijkt nu toch juist te zijn. Laughing
Mijn manier was:
AB²+BC² =AC²= AD²+DC² = 3²+4² = 9+16 = 25
AC = 5
AB²=BC² = AD²+DC²
AB²=9+16-1 = 24
AB = vierkw 24 = 4,9
opp ABC=ABXBC/2
opp ACD=ADXDC/2
oppABCD= ABXBC/2 + ADXDC/2 = [(4,9X1)+(3X4)] / 2 = (4,9+12)/2 = 8,45
Mijn manier was:
AB²+BC² =AC²= AD²+DC² = 3²+4² = 9+16 = 25
AC = 5
AB²=BC² = AD²+DC²
AB²=9+16-1 = 24
AB = vierkw 24 = 4,9
opp ABC=ABXBC/2
opp ACD=ADXDC/2
oppABCD= ABXBC/2 + ADXDC/2 = [(4,9X1)+(3X4)] / 2 = (4,9+12)/2 = 8,45
Wie op wraak zint, houdt zijn eigen wonden open.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste Oomski & Troontje ,
U hebt zeer juist gedacht , 't zijn inderdaad 8 gemeenschappelijke punten . Proficiat met uw mooie tekening Troontje !
Trouwens dit probleem is vroeger eens aan bod geweest ( vorige reeks blz 25-26 ) en dan was Pastoor wel op de hoogte ! Zou er dan toch sleet zitten op die crack ?
Groetjes
Sloeber
U hebt zeer juist gedacht , 't zijn inderdaad 8 gemeenschappelijke punten . Proficiat met uw mooie tekening Troontje !
Trouwens dit probleem is vroeger eens aan bod geweest ( vorige reeks blz 25-26 ) en dan was Pastoor wel op de hoogte ! Zou er dan toch sleet zitten op die crack ?
Groetjes
Sloeber
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste leerlingen,
goed gewerkt iedereen, proficiat voor gans de klas.
Dat discussiëren achteraf is ook altijd prettig om lezen.
Alleen ... mogen jullie zo lang opblijven thuis?
Ik lig al lang in bed als hier nog iedereen schijnt wakker te zijn.
Maar ja ... ik word een oude leraar en leerlingen blijven altijd jong.
Echt waar; toen ik begon les te geven waren mijn leerlingen 16-18 jaar
oud, en toen ik met pensioen ging waren ze nog 16-18 jaar oud.
Iets over vraag 7 met de rechthoek en de cirkel.
Eerst voor sloeberkebebo. Knap dat je nog weet dat op blz 25 van de
afgesloten topic het probleem ter sprake kwam. Ik ben gaan kijken en
wat zie ik ... het was een andere vraag.
Toen: hoeveel punten kunnen een rechthoek en een cirkel MAXIMAAL
gemeenschappelijk hebben.
Nu: hoeveel punten kunnen een rechthoek en een cirkel gemeen-
schappelijk hebben - ALLE mogelijkheden geven.
Wel een gans andere vraag sloeberkebebo.
En voor pastoor. Ik denk dat pastoor sommige gemeenschappelijke pun-
ten voor twee punten wil nemen, nml als het raakpunten zijn. Hij had dan
beter in zijn formulering het woordje 'samenvallend' gebruikt, in plaats
van gemeenschappelijk.
Leg even uit:
een rechte kan een cirkel SNIJDEN in TWEE punten,
een rechte kan een cirkel RAKEN in EEN punt
(- de twee snijpunten zijn dan 'samengevallen' in één punt-),
een rechte en een cirkel kunnen ook GEEN punten gemeen hebben.
Samengevat: rechte en cirkel kunnen 0, 1 of 2 punten gemeen hebben.
En nu naar onze rechthoek en de cirkel.
Hier zijn volgende gemeenschappelijke punten mogelijk:
0, 1, 2, 3, 4, 5, 6, 7 en 8!!!
Een opdracht(je) voor sloeberkebebo - mag het?
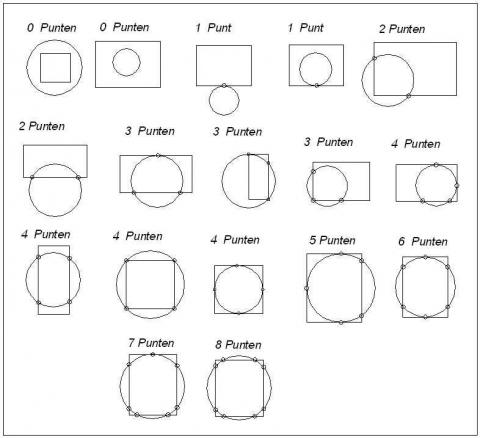
Maak NEGEN (-eventueel kleine-) figuren met telkens een andere moge-
lijkheid voor het aantal gemeenschappeljke punten, beginnend met 0
en eindigend met 8 (= figuur troontje).
Bedankt op voorhand.
tot maandag 16 november met oplossingen oefeningen getallenuitbreiding
en dinsdag 17 november voor volgende les getallenuitbreiding,
tot dan,
denook
goed gewerkt iedereen, proficiat voor gans de klas.
Dat discussiëren achteraf is ook altijd prettig om lezen.
Alleen ... mogen jullie zo lang opblijven thuis?
Ik lig al lang in bed als hier nog iedereen schijnt wakker te zijn.
Maar ja ... ik word een oude leraar en leerlingen blijven altijd jong.
Echt waar; toen ik begon les te geven waren mijn leerlingen 16-18 jaar
oud, en toen ik met pensioen ging waren ze nog 16-18 jaar oud.
Iets over vraag 7 met de rechthoek en de cirkel.
Eerst voor sloeberkebebo. Knap dat je nog weet dat op blz 25 van de
afgesloten topic het probleem ter sprake kwam. Ik ben gaan kijken en
wat zie ik ... het was een andere vraag.
Toen: hoeveel punten kunnen een rechthoek en een cirkel MAXIMAAL
gemeenschappelijk hebben.
Nu: hoeveel punten kunnen een rechthoek en een cirkel gemeen-
schappelijk hebben - ALLE mogelijkheden geven.
Wel een gans andere vraag sloeberkebebo.
En voor pastoor. Ik denk dat pastoor sommige gemeenschappelijke pun-
ten voor twee punten wil nemen, nml als het raakpunten zijn. Hij had dan
beter in zijn formulering het woordje 'samenvallend' gebruikt, in plaats
van gemeenschappelijk.
Leg even uit:
een rechte kan een cirkel SNIJDEN in TWEE punten,
een rechte kan een cirkel RAKEN in EEN punt
(- de twee snijpunten zijn dan 'samengevallen' in één punt-),
een rechte en een cirkel kunnen ook GEEN punten gemeen hebben.
Samengevat: rechte en cirkel kunnen 0, 1 of 2 punten gemeen hebben.
En nu naar onze rechthoek en de cirkel.
Hier zijn volgende gemeenschappelijke punten mogelijk:
0, 1, 2, 3, 4, 5, 6, 7 en 8!!!
Een opdracht(je) voor sloeberkebebo - mag het?
Maak NEGEN (-eventueel kleine-) figuren met telkens een andere moge-
lijkheid voor het aantal gemeenschappeljke punten, beginnend met 0
en eindigend met 8 (= figuur troontje).
Bedankt op voorhand.
tot maandag 16 november met oplossingen oefeningen getallenuitbreiding
en dinsdag 17 november voor volgende les getallenuitbreiding,
tot dan,
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goede middag allemaal ,
En nu naar onze rechthoek en de cirkel.
Hier zijn volgende gemeenschappelijke punten mogelijk:
0, 1, 2, 3, 4, 5, 6, 7 en 8!!!
Vele Groetjes en tot hoors !
Sloeber
En nu naar onze rechthoek en de cirkel.
Hier zijn volgende gemeenschappelijke punten mogelijk:
0, 1, 2, 3, 4, 5, 6, 7 en 8!!!

Vele Groetjes en tot hoors !
Sloeber
Meten is weten - Carpe diem
-
WhiteBullet - Lid geworden op: 15 nov 2009, 20:21
- Locatie: 9220 Hamme
Beste wiskundige knobbels 
Ik kom me graag met jullie meten.
Hopelijk vind ik hier steeds te tijd voor.
Op aanraden van denook heb ik me ingeschreven.
heb ik me ingeschreven.
Daarbij dank ik hem ook voor het plaatsen van mijn vraagstuk betreffende de bus vol kinderen.
Tot volgende berichtgeving
En toi toi toi voor iedereen
Ik kom me graag met jullie meten.
Hopelijk vind ik hier steeds te tijd voor.
Op aanraden van denook
Daarbij dank ik hem ook voor het plaatsen van mijn vraagstuk betreffende de bus vol kinderen.
Tot volgende berichtgeving
En toi toi toi voor iedereen