Wiskundige problemen en probleempjes 2
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste Pastoor ,
Ook bij U is de vis gevangen ! !
Dit is volledig juist en zeer prachtig uitgelegd ! !
De crack is nog niet versleten .
Groetjes
Sloeber
Ook bij U is de vis gevangen ! !
Dit is volledig juist en zeer prachtig uitgelegd ! !
De crack is nog niet versleten .
Groetjes
Sloeber
Meten is weten - Carpe diem
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Voor iedereen die graag rekent !

Groetjes
Sloeber
PS De hoek is een rechte hoek !

Groetjes
Sloeber
PS De hoek is een rechte hoek !
Laatst gewijzigd door sloeberkebebo op 20 nov 2009, 12:29, 3 keer totaal gewijzigd.
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
probleem van sloeber,
als er onbekenden zijn, moet men altijd trachten vergelijkingen
te vinden, evenveel als er onbekenden zijn.
Hier zijn 3 onbekenden; dus zoeken we 3 vergelijkingen.
1) A en B zijn samen 100, dus vergelijking 1:
B = 100 - A
2) Ik denk dat de aangeduide hoek 90° is, alhoewel moeilijk leesbaar;
dus Pythagoras geeft vergelijking 2:
A² + C² = B²
3) Tenslotte zijn er twee GELIJKVORMIGE driehoeken, dwz dat de
breuken van overeenkomstige zijden steeds gelijk zijn.
De driehoeken zijn de grote driehoek met zijden A, B en C
en de driehoek boven het gekleurde vierkant gelegen.
Wat zijn dan o.a. overkomstige zijden?
A en A-10,
C en 10
dat geeft dan A/A-10 = C/10,
of 10A = C.(A-10)
zo krijgen we vergelijking 3:
10A = C.A - 10C
met deze drie vergelijkingen kunnen we nu verder zoeken,
groetjes,
denook
ps. Als de hoek geen 90° is, zoals moeilijk te lezen, doch 98°,
dan wordt vergelijking 2 (-met Pythagoras), een vergelijking
steunend op de cosinusregel; dit wordt dan
B² = A² + C² - 2A.C.cos98°
Ik denk niet dat dit de bedoeling is.
nog een ps. ziet iemand een kortere of gemakkelijkere methode
(-pastoor?-): DOEN
als er onbekenden zijn, moet men altijd trachten vergelijkingen
te vinden, evenveel als er onbekenden zijn.
Hier zijn 3 onbekenden; dus zoeken we 3 vergelijkingen.
1) A en B zijn samen 100, dus vergelijking 1:
B = 100 - A
2) Ik denk dat de aangeduide hoek 90° is, alhoewel moeilijk leesbaar;
dus Pythagoras geeft vergelijking 2:
A² + C² = B²
3) Tenslotte zijn er twee GELIJKVORMIGE driehoeken, dwz dat de
breuken van overeenkomstige zijden steeds gelijk zijn.
De driehoeken zijn de grote driehoek met zijden A, B en C
en de driehoek boven het gekleurde vierkant gelegen.
Wat zijn dan o.a. overkomstige zijden?
A en A-10,
C en 10
dat geeft dan A/A-10 = C/10,
of 10A = C.(A-10)
zo krijgen we vergelijking 3:
10A = C.A - 10C
met deze drie vergelijkingen kunnen we nu verder zoeken,
groetjes,
denook
ps. Als de hoek geen 90° is, zoals moeilijk te lezen, doch 98°,
dan wordt vergelijking 2 (-met Pythagoras), een vergelijking
steunend op de cosinusregel; dit wordt dan
B² = A² + C² - 2A.C.cos98°
Ik denk niet dat dit de bedoeling is.
nog een ps. ziet iemand een kortere of gemakkelijkere methode
(-pastoor?-): DOEN
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste rekenaars .
Het is wel degelijk een rechte hoek !
Letters & cijfers aangepast in de figuur !
mvg Sloeber
Het is wel degelijk een rechte hoek !
Letters & cijfers aangepast in de figuur !
mvg Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Meester Denook,
Nee, had dezelfde 3 vergelijkingen.
En dan wat berekenen met cosinus- en sinusregel, en dit laten vallen want het levert niets.
Blijft over een 3e graadsvergelijking.
Ik ga nu proberen die vergelijking op te lossen.
Sloeberkebebo heeft weer een "monstertje" geleverd.
Nee, had dezelfde 3 vergelijkingen.
En dan wat berekenen met cosinus- en sinusregel, en dit laten vallen want het levert niets.
Blijft over een 3e graadsvergelijking.
Ik ga nu proberen die vergelijking op te lossen.
Sloeberkebebo heeft weer een "monstertje" geleverd.
Sudoku, wijntjes proeven, genieten.
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
De drie vergelijkingen.
A² + C² = B² (1).
B = 100 – A (2).
C = 10A /(A-10) (3).
De berekening van A.
(3) en (2) in (1).
A² + ((10A)/(A-10))² = (100 – A)²
A² + (100A²/ (A² - 20A +100)) = 10000 – 200A + A².
100A²/ (A² - 20A +100)) - 10000 + 200A = 0
A²/ (A² - 20A +100)) - 100 + 2A = 0
A² - 100A² + 2A³ + 2000A - 40A² - 10000 +200A = 0
2A³ - 139A² + 2200A -10000 = 0
A³ - 69,5A² + 1100A – 5000 = 0. is een derdegraads vergelijking, dus 3 oplossingen.
Oplossen derde graadsvergeliijking.
Transformaties.
Stel: (a = 1), (b = -69,5), (c = 1100), (d = -5000), (A = x).
Dat levert: ax³ + bx² + cx + d = 0
In die vergelijking nu x vervangen door (y – (b/3a))
En het resultaat delen door a.
Dat levert: y³ +py + q = 0.
Dan is y = een reële wortel =
(de derdemachtwortel van (-q/2 + √((q/2)² + (p/3)³))
+ (de derdemachtswortel van (-q/2 - √((q/2)² + (p/3)³)).
(Als de uitdrukking onder de vierkantswortel negatief is, dan zijn er 2 complexe getallen de 2e en 3e oplossong).
De berekening van B.
B = 100 – A
De berekening van C.
C = 10A /(A-10)
* * * * * *
Een veel eenvoudigere oplossing is "A³ - 69,5A² + 1100A – 5000 = 0." te programmeren op een mainframe in de talen Cobol of assembler met:
de variabele A
die varieert van een initiële waarde 0,000001
met een increment van 0,000001
tot het resultaat 0 bereikt wordt voor een bepaalde A waarde
en de A waarde moet onder de 100 blijven.
* * *
A² + C² = B² (1).
B = 100 – A (2).
C = 10A /(A-10) (3).
De berekening van A.
(3) en (2) in (1).
A² + ((10A)/(A-10))² = (100 – A)²
A² + (100A²/ (A² - 20A +100)) = 10000 – 200A + A².
100A²/ (A² - 20A +100)) - 10000 + 200A = 0
A²/ (A² - 20A +100)) - 100 + 2A = 0
A² - 100A² + 2A³ + 2000A - 40A² - 10000 +200A = 0
2A³ - 139A² + 2200A -10000 = 0
A³ - 69,5A² + 1100A – 5000 = 0. is een derdegraads vergelijking, dus 3 oplossingen.
Oplossen derde graadsvergeliijking.
Transformaties.
Stel: (a = 1), (b = -69,5), (c = 1100), (d = -5000), (A = x).
Dat levert: ax³ + bx² + cx + d = 0
In die vergelijking nu x vervangen door (y – (b/3a))
En het resultaat delen door a.
Dat levert: y³ +py + q = 0.
Dan is y = een reële wortel =
(de derdemachtwortel van (-q/2 + √((q/2)² + (p/3)³))
+ (de derdemachtswortel van (-q/2 - √((q/2)² + (p/3)³)).
(Als de uitdrukking onder de vierkantswortel negatief is, dan zijn er 2 complexe getallen de 2e en 3e oplossong).
De berekening van B.
B = 100 – A
De berekening van C.
C = 10A /(A-10)
* * * * * *
Een veel eenvoudigere oplossing is "A³ - 69,5A² + 1100A – 5000 = 0." te programmeren op een mainframe in de talen Cobol of assembler met:
de variabele A
die varieert van een initiële waarde 0,000001
met een increment van 0,000001
tot het resultaat 0 bereikt wordt voor een bepaalde A waarde
en de A waarde moet onder de 100 blijven.
* * *
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste Pastoor ,
"" En dan wat berekenen met cosinus- en sinusregel, en dit laten vallen want het levert niets. ""
Tangens bestaat ook nog !
Niet te rap een conclusie trekken , men kan ook rekenen met een Basic programmaatje of ook met een programeerbare rekenmachine ! Een mainframe is toch wel wat hoog gegrepen volgens mij . Rekenen is zo plezant , maar die oefeningen zijn zo ambetant !
mvg
Sloeber
"" En dan wat berekenen met cosinus- en sinusregel, en dit laten vallen want het levert niets. ""
Tangens bestaat ook nog !
Niet te rap een conclusie trekken , men kan ook rekenen met een Basic programmaatje of ook met een programeerbare rekenmachine ! Een mainframe is toch wel wat hoog gegrepen volgens mij . Rekenen is zo plezant , maar die oefeningen zijn zo ambetant !
mvg
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Sloeberkebebo
Van de rechthoekige driehoek met zijden A, B, en C is enkel de rechte hoek van 90° gekend.
Sinus, cosinus, tangens, zijn aanduidingen van de verhouding van lengtes van lijnstukken.
Stel rechthoekige driehoek, en stel a de hoek (snijpunt C en B).
sin a = C/B, cos a = A/B , tg a = C/A. cotg = A/C. (niets gekend).
Men kan een rechthoekige driehoek oplossen als men:
* één scherpe hoek kent en (schuine zijde OF rechthoekszijde). Geen scherpe hoek gekend.
*een schuine zijde en rechthoekszijde kent. Beiden niet gekend.
Als men dat zou meten, dan is het zo opgelost. Uw computer kijkt niet naar die 10. Die meet de lengte van A, B, en C en kent de rechte hoek en de andere hoeken en begint te rekenen.
In wiskunde kan men niet meten, alleen tellen. Ik zou kunnen zeggen A is bijna gelijk aan B, maar met het woord "bijna" kan men niet tellen.
Daarom 3 vergelijkingen met 3 onbekenden en een derde graadsvergelijking. Dat wat ik geschreven heb komt van het internet.
* * * * *
Daarboven stond: A³ - 69,5A² + 1100A – 5000 = 0
of ax³ + bx² + cx + d = 0
Of x³ + (b/a)x² + (c/a)x + (d/a) = 0
Of x³ + fx³ + gx + h = 0
Dan kan men zeggen:
Ik heb nu x³+fx²+gx+h=0.
Stel dat a, b en c de wortels van die vergelijking zijn,
dan is x³+fx+gx+h = (x-a)(x-b)(x-c).
En als men dat uitwerkt dan is f=-(a+b+c), g=(ab+bc+ac) en h=(-abc).
Juist of niet. Meester Denook weet dit maar al te goed.
Maar reken het maar uit.
* * * * *
Waarom die mainframe, er zijn "20 quadrillion instructies" computers, even snel als 2.000.000 labtops tesamen. Of omgerekend doet die mainframe in 8 uren even veel als een labtop in 20.000 jaren.
(maar dan alleen floating-points berekeningen).
Van de rechthoekige driehoek met zijden A, B, en C is enkel de rechte hoek van 90° gekend.
Sinus, cosinus, tangens, zijn aanduidingen van de verhouding van lengtes van lijnstukken.
Stel rechthoekige driehoek, en stel a de hoek (snijpunt C en B).
sin a = C/B, cos a = A/B , tg a = C/A. cotg = A/C. (niets gekend).
Men kan een rechthoekige driehoek oplossen als men:
* één scherpe hoek kent en (schuine zijde OF rechthoekszijde). Geen scherpe hoek gekend.
*een schuine zijde en rechthoekszijde kent. Beiden niet gekend.
Als men dat zou meten, dan is het zo opgelost. Uw computer kijkt niet naar die 10. Die meet de lengte van A, B, en C en kent de rechte hoek en de andere hoeken en begint te rekenen.
In wiskunde kan men niet meten, alleen tellen. Ik zou kunnen zeggen A is bijna gelijk aan B, maar met het woord "bijna" kan men niet tellen.
Daarom 3 vergelijkingen met 3 onbekenden en een derde graadsvergelijking. Dat wat ik geschreven heb komt van het internet.
* * * * *
Daarboven stond: A³ - 69,5A² + 1100A – 5000 = 0
of ax³ + bx² + cx + d = 0
Of x³ + (b/a)x² + (c/a)x + (d/a) = 0
Of x³ + fx³ + gx + h = 0
Dan kan men zeggen:
Ik heb nu x³+fx²+gx+h=0.
Stel dat a, b en c de wortels van die vergelijking zijn,
dan is x³+fx+gx+h = (x-a)(x-b)(x-c).
En als men dat uitwerkt dan is f=-(a+b+c), g=(ab+bc+ac) en h=(-abc).
Juist of niet. Meester Denook weet dit maar al te goed.
Maar reken het maar uit.
* * * * *
Waarom die mainframe, er zijn "20 quadrillion instructies" computers, even snel als 2.000.000 labtops tesamen. Of omgerekend doet die mainframe in 8 uren even veel als een labtop in 20.000 jaren.
(maar dan alleen floating-points berekeningen).
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste pastoor, sloeberkebebo en allen die nog meevolgen ...
Alles wat pastoor hier schrijft is juist. Hoe kan ik dan nog aanvullen?
Wel, als je een vergelijking hebt van de hogere graad, dan bestaat er
geen formule om daar de oplossingen van te vinden.
Er is zelfs bewezen dat men geen formule kan vinden om bv een alge-
mene vergelijking van de vijfde graad op te lossen.
Er bestaan nu wel methoden om de oplossing van een dergelijke verge-
lijking te benaderen, tot op 2, 3, 4, ... cijfers na de komma nauwkeurig.
In de moderne rekentoestellen die wat aankunnen zit een van deze
methoden ingebouwd.
Je tikt gewoon achtereenvolgens al de coëfficiënten (= de getallesn die bij
de machten van x staan) in, en een goede benadering van de oplossing
komt er zo uit.
vb. bij 3x-tot de vierde - 13x³ - x² + 53x - 42 = 0,
tik je in 3, -13, -1, 53, -42 en er zal o.a. verschijnen x = 2,33...
dit als benadering van een oplossing.
Ik heb zo'n rekenmachientje niet.
Vroeger hadden de leerlingen dat ook niet.
Wij werkten dus met de benaderingsmethoden zelf om de oplossingen
te vinden. Er werden zo drie methoden aangeleerd en de leerlingen
werkten met de methode die hen best lag.
Ik berekende, steunend op de laatste vergelijking van de derde graad
van pastoor, met een van de methoden, dat een benaderde waarde
voor A, 49,21 was. Is ze juist sloeberkebebo?
Dan is B = 100 - A en C vindt men uit C² = B² - A².
We onthouden: met een rekenmachientje gaat het vlug,
doch het blijven benaderingen.
Is ok, want er is geen exacte formule te vinden.
We blijven ook onze voorouders gedenken die het allemaal zonder
rekenmachientje moesten klaren en er ook geraakten ...
groetjes en tot dinsdag,
denook
Alles wat pastoor hier schrijft is juist. Hoe kan ik dan nog aanvullen?
Wel, als je een vergelijking hebt van de hogere graad, dan bestaat er
geen formule om daar de oplossingen van te vinden.
Er is zelfs bewezen dat men geen formule kan vinden om bv een alge-
mene vergelijking van de vijfde graad op te lossen.
Er bestaan nu wel methoden om de oplossing van een dergelijke verge-
lijking te benaderen, tot op 2, 3, 4, ... cijfers na de komma nauwkeurig.
In de moderne rekentoestellen die wat aankunnen zit een van deze
methoden ingebouwd.
Je tikt gewoon achtereenvolgens al de coëfficiënten (= de getallesn die bij
de machten van x staan) in, en een goede benadering van de oplossing
komt er zo uit.
vb. bij 3x-tot de vierde - 13x³ - x² + 53x - 42 = 0,
tik je in 3, -13, -1, 53, -42 en er zal o.a. verschijnen x = 2,33...
dit als benadering van een oplossing.
Ik heb zo'n rekenmachientje niet.
Vroeger hadden de leerlingen dat ook niet.
Wij werkten dus met de benaderingsmethoden zelf om de oplossingen
te vinden. Er werden zo drie methoden aangeleerd en de leerlingen
werkten met de methode die hen best lag.
Ik berekende, steunend op de laatste vergelijking van de derde graad
van pastoor, met een van de methoden, dat een benaderde waarde
voor A, 49,21 was. Is ze juist sloeberkebebo?
Dan is B = 100 - A en C vindt men uit C² = B² - A².
We onthouden: met een rekenmachientje gaat het vlug,
doch het blijven benaderingen.
Is ok, want er is geen exacte formule te vinden.
We blijven ook onze voorouders gedenken die het allemaal zonder
rekenmachientje moesten klaren en er ook geraakten ...
groetjes en tot dinsdag,
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Hier dan de oplossing van de omvergevallen vlaggemast !
Beste allemaal
Bereken de waarden : Manueel , met rekenmachine of met de computer ……….of teken het gewoon met de computer .

Neem de kleinste hoek ( H ) van de rode driehoek als beginwaarde !
Neem als begin waarde 50 en 10 en bereken hoek H en
neem deze hoek H als begin waarde voor de berekeningen .
( deze is altijd te klein t.o.v. van deze die we zoeken )
PS : Hier zeer rap een eenvoudig Basic programmaatje geschreven voor GW-Basic voor op de computer : zie in de zwarte kader ( kan ook op uw computer )
Met de computer via Basic programma “ GW-Basic “ .
Input “ Begin hoek = 11.31 “
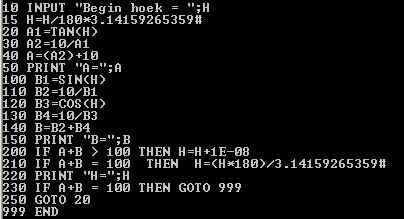
Na ongeveer een kwartier rekenen
Eind resultaat :

A= (10/tan H ) + 10
B= (10/sin H ) + ( 10/cos H )
A+B = 100
If A+B > 100 then H ===> te klein
A= 49,21247
B= 50,78754
H = 14,30668
B² - A² = C² ====> C = 12,55021
Met wat rekenwerk vind U zo de oplossing
Veel reken plezier
Groetjes
Sloeberkebebo ( Ik ben toch een sloeber of niet ? )

Nota : Bijna niemand kent nog het spijkerschrift en heeft nog een hamer en een beitel om het te beitelen in steen !
Beste allemaal
Bereken de waarden : Manueel , met rekenmachine of met de computer ……….of teken het gewoon met de computer .

Neem de kleinste hoek ( H ) van de rode driehoek als beginwaarde !
Neem als begin waarde 50 en 10 en bereken hoek H en
neem deze hoek H als begin waarde voor de berekeningen .
( deze is altijd te klein t.o.v. van deze die we zoeken )
PS : Hier zeer rap een eenvoudig Basic programmaatje geschreven voor GW-Basic voor op de computer : zie in de zwarte kader ( kan ook op uw computer )
Met de computer via Basic programma “ GW-Basic “ .
Input “ Begin hoek = 11.31 “

Na ongeveer een kwartier rekenen
Eind resultaat :

A= (10/tan H ) + 10
B= (10/sin H ) + ( 10/cos H )
A+B = 100
If A+B > 100 then H ===> te klein
A= 49,21247
B= 50,78754
H = 14,30668
B² - A² = C² ====> C = 12,55021
Met wat rekenwerk vind U zo de oplossing
Veel reken plezier
Groetjes
Sloeberkebebo ( Ik ben toch een sloeber of niet ? )

Nota : Bijna niemand kent nog het spijkerschrift en heeft nog een hamer en een beitel om het te beitelen in steen !
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste sloeber,
want dat ben je inderdaad.
Je laatste 'nota' van je artikel hierboven voel ik een beetje aan als een
ridiculiseren van mijn laatste zin in mijn laatste artikeltje hier.
Dat mag, ik heb daar zeker geen moeite mee.
Wel denk ik, als ik vergelijk met de veertiendaagse wiskundeproblemen,
dat je een beetje boven de hoofden schrijft van ons, leerlingen en leraar
hier.
Op bepaalde terreinen ben je een crack, waar wij niet tegenaan kunnen.
Vernieuwing is nodig, betere technieken zijn nodig, minder zware handen-
arbeid is nodig, gebruik van de nieuwste, onvoorstelbaar mooie prgram-
ma's zijn nodig ... dat is allemaal nodig!!
Toch mogen we onze herkomst, het werk van de pioniers vóór ons, nooit
verloochenen. Zonder hun werk stonden we nu nog bijna nergens.
Ik heb weinig 'straffe' wiskunde-programma's; wel enkele.
Dat heeft ook te maken met het niet meer 'actief' zijn op het terrein.
Jouw laatste probleem loste ik op zoals vroeger, zonder computer en
computerproramma's, wel met een heel gewoon rekenmachientje.
Ik dacht dat we moesten rekenen met 2 decimalen, zoals je vorige oef.
Ik vond voor A de waarde 49,212, alle cijfers juist zoals nu blijkt; ik dacht
met één cijfer te veel, doch het was met 2 cijfers te weinig, las ik nu.
Om tot die waarde 49,212 te komen had ik ook minder dan 15 minuten
nodig; met nog 5 minuten erbij kwam ik ook tot 5 decimalen; zeker!
Maar, beste sloeber(kebebo), we moeten alle hulpmiddelen die de moder-
ne technologie ons biedt, ook leren gebruiken. Daar sta ik volledig achter
jou. Alleen ... ik ben geen computerfreak, en voel ook niet de noodzaak
om op mijn gezegende leeftijd, me er nog volop in te verdiepen.
Mijn dagen zijn meer dan gevuld, ook met een paar passionele hobby!s,
buiten de wiskunde om, en zo is het goed, meer dan goed.
Mag ik eindigen met mijn bewondering te uiten voor al het knappe dat
jij hier naar voor brengt. Chapeau!!
groetjes iedereen en
nog eens ... tot dinsdag,
denook
want dat ben je inderdaad.
Je laatste 'nota' van je artikel hierboven voel ik een beetje aan als een
ridiculiseren van mijn laatste zin in mijn laatste artikeltje hier.
Dat mag, ik heb daar zeker geen moeite mee.
Wel denk ik, als ik vergelijk met de veertiendaagse wiskundeproblemen,
dat je een beetje boven de hoofden schrijft van ons, leerlingen en leraar
hier.
Op bepaalde terreinen ben je een crack, waar wij niet tegenaan kunnen.
Vernieuwing is nodig, betere technieken zijn nodig, minder zware handen-
arbeid is nodig, gebruik van de nieuwste, onvoorstelbaar mooie prgram-
ma's zijn nodig ... dat is allemaal nodig!!
Toch mogen we onze herkomst, het werk van de pioniers vóór ons, nooit
verloochenen. Zonder hun werk stonden we nu nog bijna nergens.
Ik heb weinig 'straffe' wiskunde-programma's; wel enkele.
Dat heeft ook te maken met het niet meer 'actief' zijn op het terrein.
Jouw laatste probleem loste ik op zoals vroeger, zonder computer en
computerproramma's, wel met een heel gewoon rekenmachientje.
Ik dacht dat we moesten rekenen met 2 decimalen, zoals je vorige oef.
Ik vond voor A de waarde 49,212, alle cijfers juist zoals nu blijkt; ik dacht
met één cijfer te veel, doch het was met 2 cijfers te weinig, las ik nu.
Om tot die waarde 49,212 te komen had ik ook minder dan 15 minuten
nodig; met nog 5 minuten erbij kwam ik ook tot 5 decimalen; zeker!
Maar, beste sloeber(kebebo), we moeten alle hulpmiddelen die de moder-
ne technologie ons biedt, ook leren gebruiken. Daar sta ik volledig achter
jou. Alleen ... ik ben geen computerfreak, en voel ook niet de noodzaak
om op mijn gezegende leeftijd, me er nog volop in te verdiepen.
Mijn dagen zijn meer dan gevuld, ook met een paar passionele hobby!s,
buiten de wiskunde om, en zo is het goed, meer dan goed.
Mag ik eindigen met mijn bewondering te uiten voor al het knappe dat
jij hier naar voor brengt. Chapeau!!
groetjes iedereen en
nog eens ... tot dinsdag,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
dinsdag 24 november,
volgende reeks problemen en probleempjes.
1) Op een digitaal uurwerk lees ik om middernacht als tijdstip, 00:00:00.
Hoe laat is het als de eerstvolgende keer een tijdstip leesbaar is waar geen ‘0’ in voorkomt?
2) Het mosselhuis ‘Dik-lekker-sappig’ bestaat twintig jaar. In een stuntcampagne geven ze volgende promotie: ‘bij aankoop van drie kilo mosselen krijg je 25% korting en betaal je 9 euro’. Hoeveel betaal je voor één kilogram mosselen, vóór de promotie?
4) Als n² = m! + 1 ( weet je nog, m! = 1.2.3. … .m ),
dan zijn er verschillende koppels m- en n-waarden die hieraan voldoen.
Geef twee verschillende juiste m- en n-waarden voor de formule.
5) Beschouw een regelmatige achthoek.
Hoeveel driehoeken kan je vormen met als zijden, diagonalen van de achthoek?
6) Hermine legt met lucifers een vierkant. Daarna maakt ze een vierkant, door kleine vierkantjes aan te leggen. Zo gaat ze door tot en met vierkant 31.
Hieronder zie je de vierkanten 1, 2 en 3.
Hoeveel lucifers heeft vierkant 31 meer dan 30?
7) Ik kom Bart tegen, van wie ik weet dat hij twee kindjes heeft; een ervan is bij hem. “Dit is mijn zoon Lucas”, zegt Bart. Als je dat weet, hoe groot is dan de kans dat ook zijn tweede kind een jongen is? ( we nemen aan dat bij de geboorte de kans op een jongen en een meisje even groot is ).
- dit probleempje is meer dan 200 jaar oud en zorgde heel lang voor discussie –
8 ) Als A, B, C en D cijfers zijn en het getal geschreven als ABCD, vermenigvuldigd met 9, het getal DCBA geeft, wat zijn dan de cijfers A, B, C en D?
9) Eén van de gezondheidsindicatoren die zeer veel in het nieuws komen is de Body Mass Index: BMI = (gewicht persoon in kg) / (lengte persoon in meter)².
Recent werd weer een topmodel geweigerd omdat haar BMI kleiner was dan 18.
Ze meet 1,80 meter en weegt 54,32 kg.
Hoeveel moet ze verzwaren om niet te worden geweigerd?
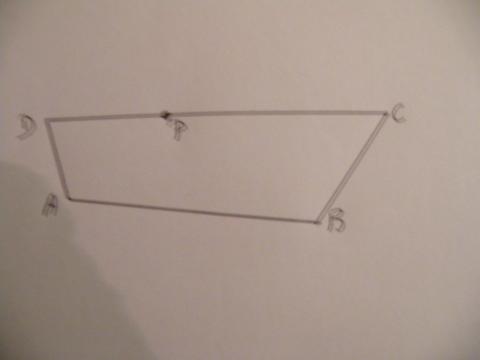
10) ABCD is een willekeurige vierhoek, zoals op onderstaande figuur. Op CD leg je willekeurig een punt P.
Teken AP en een evenwijdige door D aan AP,
Teken ook BP en een evenwijdige door C aan BP.
De twee evenwijdigen snijden elkaar in S.
Toon aan dat de oppervlakte van driehoek ABS gelijk is aan de oppervlakte van ABCD.
Veel succes iedereen, en … nieuwe leerlingen lezen eerst blz 1 van deze topic.
Tot morgen …
denook
volgende reeks problemen en probleempjes.
1) Op een digitaal uurwerk lees ik om middernacht als tijdstip, 00:00:00.
Hoe laat is het als de eerstvolgende keer een tijdstip leesbaar is waar geen ‘0’ in voorkomt?
2) Het mosselhuis ‘Dik-lekker-sappig’ bestaat twintig jaar. In een stuntcampagne geven ze volgende promotie: ‘bij aankoop van drie kilo mosselen krijg je 25% korting en betaal je 9 euro’. Hoeveel betaal je voor één kilogram mosselen, vóór de promotie?
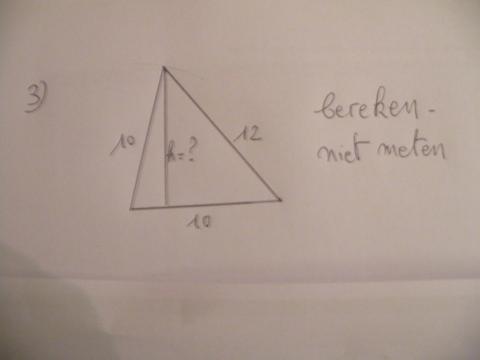
4) Als n² = m! + 1 ( weet je nog, m! = 1.2.3. … .m ),
dan zijn er verschillende koppels m- en n-waarden die hieraan voldoen.
Geef twee verschillende juiste m- en n-waarden voor de formule.
5) Beschouw een regelmatige achthoek.
Hoeveel driehoeken kan je vormen met als zijden, diagonalen van de achthoek?
6) Hermine legt met lucifers een vierkant. Daarna maakt ze een vierkant, door kleine vierkantjes aan te leggen. Zo gaat ze door tot en met vierkant 31.
Hieronder zie je de vierkanten 1, 2 en 3.
Hoeveel lucifers heeft vierkant 31 meer dan 30?

7) Ik kom Bart tegen, van wie ik weet dat hij twee kindjes heeft; een ervan is bij hem. “Dit is mijn zoon Lucas”, zegt Bart. Als je dat weet, hoe groot is dan de kans dat ook zijn tweede kind een jongen is? ( we nemen aan dat bij de geboorte de kans op een jongen en een meisje even groot is ).
- dit probleempje is meer dan 200 jaar oud en zorgde heel lang voor discussie –
8 ) Als A, B, C en D cijfers zijn en het getal geschreven als ABCD, vermenigvuldigd met 9, het getal DCBA geeft, wat zijn dan de cijfers A, B, C en D?
9) Eén van de gezondheidsindicatoren die zeer veel in het nieuws komen is de Body Mass Index: BMI = (gewicht persoon in kg) / (lengte persoon in meter)².
Recent werd weer een topmodel geweigerd omdat haar BMI kleiner was dan 18.
Ze meet 1,80 meter en weegt 54,32 kg.
Hoeveel moet ze verzwaren om niet te worden geweigerd?
10) ABCD is een willekeurige vierhoek, zoals op onderstaande figuur. Op CD leg je willekeurig een punt P.
Teken AP en een evenwijdige door D aan AP,
Teken ook BP en een evenwijdige door C aan BP.
De twee evenwijdigen snijden elkaar in S.
Toon aan dat de oppervlakte van driehoek ABS gelijk is aan de oppervlakte van ABCD.

Veel succes iedereen, en … nieuwe leerlingen lezen eerst blz 1 van deze topic.
Tot morgen …
denook
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
Beste denook,
2) Het mosselhuis ‘Dik-lekker-sappig’ bestaat twintig jaar. In een stuntcampagne geven ze volgende promotie: ‘bij aankoop van drie kilo mosselen krijg je 25% korting en betaal je 9 euro’. Hoeveel betaal je voor één kilogram mosselen, vóór de promotie?
1 kg mossels 3€ = 75 % van 4€
prijs per kg mossels voor de promotie 4€
groetjes aan iedereen
lotte
2) Het mosselhuis ‘Dik-lekker-sappig’ bestaat twintig jaar. In een stuntcampagne geven ze volgende promotie: ‘bij aankoop van drie kilo mosselen krijg je 25% korting en betaal je 9 euro’. Hoeveel betaal je voor één kilogram mosselen, vóór de promotie?
1 kg mossels 3€ = 75 % van 4€
prijs per kg mossels voor de promotie 4€
groetjes aan iedereen
lotte
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goeden avond allemaal
vraag 6
volgens mij zijn er 124 lucifers meer t.o.v. vierkant 30
groetjes
Sloeber
vraag 6
volgens mij zijn er 124 lucifers meer t.o.v. vierkant 30
groetjes
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
4) Als n² = m! + 1 ( weet je nog, m! = 1.2.3. … .m ),
dan zijn er verschillende koppels m- en n-waarden die hieraan voldoen.
Geef twee verschillende juiste m- en n-waarden voor de formule.
n =5, m = 4
n = 11, m = 5
dan zijn er verschillende koppels m- en n-waarden die hieraan voldoen.
Geef twee verschillende juiste m- en n-waarden voor de formule.
n =5, m = 4
n = 11, m = 5
Sudoku, wijntjes proeven, genieten.