Wiskundige problemen en probleempjes 2
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Avond allemaal.
Vraag 5 Beschouw een regelmatige achthoek. Hoeveel driehoeken kan je vormen met als zijden, diagonalen van de achthoek?
Dus driehoeken waarvan de zijden diagonalen zijn.
Een regelmatige driehoek, vierhoek, en vijfhoek heeft dat niet.
Een regelmatige zeshoek levert 2 driehoeken gemaakt van diagonalen.
(men kan er drie maken, maar dan is er een duplicaat, wat niet mag)
Een regelmatige zevenhoek levert 7 driehoeken gemaakt van diagonalen.
In een regelmatige achthoek kan men 12 driehoeken maken met de diagonalen.
Vraag 5 Beschouw een regelmatige achthoek. Hoeveel driehoeken kan je vormen met als zijden, diagonalen van de achthoek?
Dus driehoeken waarvan de zijden diagonalen zijn.
Een regelmatige driehoek, vierhoek, en vijfhoek heeft dat niet.
Een regelmatige zeshoek levert 2 driehoeken gemaakt van diagonalen.
(men kan er drie maken, maar dan is er een duplicaat, wat niet mag)
Een regelmatige zevenhoek levert 7 driehoeken gemaakt van diagonalen.
In een regelmatige achthoek kan men 12 driehoeken maken met de diagonalen.
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Oplossingen volgens meester Denook

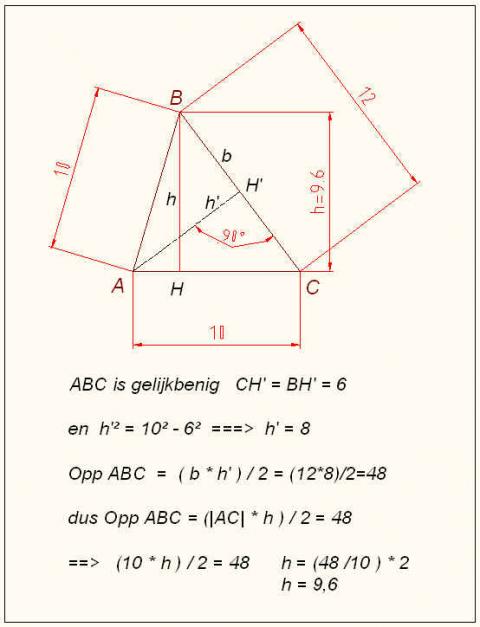


Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
sorry, ben wat koortsig en ... in slaap gevallen.
vraag 9) sloeberkebebo - ok
+ mooi figuurtje
vraag 1) lotte - ok
vraag 5) pastoor - niet juist.
de andere veelhoeken die je aanaalt zijn juist;
de achthoek niet.
Iedereen op zoek naar dit laatste vraagje ...
bedankt sloeberkebebo voor de twee prachtige tekeningen,
denook
sorry, ben wat koortsig en ... in slaap gevallen.
vraag 9) sloeberkebebo - ok
+ mooi figuurtje
vraag 1) lotte - ok
vraag 5) pastoor - niet juist.
de andere veelhoeken die je aanaalt zijn juist;
de achthoek niet.
Iedereen op zoek naar dit laatste vraagje ...
bedankt sloeberkebebo voor de twee prachtige tekeningen,
denook
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Vraag 5. driemaal apart opnieuw gedaan, telkens 11.
Noem de hoeken 1, 2, 3, 4, 5, 6, 7, 8.
diagonaaldriehoeken.
(1) 1-3-5.
(2) 1-4-6.
(3) 1–5–7.
(4) 2–4-6.
(5) 2–5–7.
(6) 2–6–8.
(7) 3-5-7.
( 8 ) 3-6-8.
(9) 4-6-8 .
(10) 4-7-2.
(11) 5-8-3.
Noem de hoeken 1, 2, 3, 4, 5, 6, 7, 8.
diagonaaldriehoeken.
(1) 1-3-5.
(2) 1-4-6.
(3) 1–5–7.
(4) 2–4-6.
(5) 2–5–7.
(6) 2–6–8.
(7) 3-5-7.
( 8 ) 3-6-8.
(9) 4-6-8 .
(10) 4-7-2.
(11) 5-8-3.
Laatst gewijzigd door pastoor op 27 nov 2009, 23:46, 2 keer totaal gewijzigd.
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Even proberen voor vraag 5...............
Laatst gewijzigd door sloeberkebebo op 28 nov 2009, 09:54, 3 keer totaal gewijzigd.
Meten is weten - Carpe diem
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
vraag 5
Noem de hoeken ABCDEFGH
De diagonaaldriehoeken zijn
1) ACG
2) ADF
3) BDH
4) BEG
5) CFH
Als wij nog diagonaaldriehoeken willen maken moet men reeds gebruikte diagonalen gebruiken .
Sloeber
Noem de hoeken ABCDEFGH
De diagonaaldriehoeken zijn
1) ACG
2) ADF
3) BDH
4) BEG
5) CFH
Als wij nog diagonaaldriehoeken willen maken moet men reeds gebruikte diagonalen gebruiken .
Sloeber
Meten is weten - Carpe diem
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
Beste denook en allen
nog iets anders voor vraag 5
heb een achthoek getekend en gezien hoeveel driehoeken je kunt tekenen vanuit één hoekpunt = 6
er zijn acht hoekpunten = 6*8
elke driehoek komt in 3 verschillende hoekpunten toe = /3
(6*8)/3 = 16 driehoeken ?
groetjes
lotte.
nog iets anders voor vraag 5
heb een achthoek getekend en gezien hoeveel driehoeken je kunt tekenen vanuit één hoekpunt = 6
er zijn acht hoekpunten = 6*8
elke driehoek komt in 3 verschillende hoekpunten toe = /3
(6*8)/3 = 16 driehoeken ?
groetjes
lotte.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
hallo beste leerlingen,
wat een problemen met die simpele achthoek en de driehoeken.
Het is onbegonnen werk om ze allemaal te willen tekenen - zou zeer
verwarrend zijn.
Belangrijk voor men start: in ieder van de acht hoekpunten moeten
evenveel driehoeken een hoekpunt hebben.
Zo kan het niet pastoor dat bij jou in punt 1, drie driehoeken komen
en in punt 6 komen er vijf toe.
Sloeberkebebo, eenzelfde diagonaal kan toch zijde zijn van meerdere
driehoeken!
Starten we met de nummering van pastoor; hoekpunten 1, 2, ... tot 8.
We tekenen alle driehoeken waar punt 1 een hoekpunt van is:
(1, 3, 5), (1, 3, 6), (1, 3, 7), (1, 4, 6), (1, 4, 7) en (1, 5, 7).
Dat zijn ze allemaal, zes in totaal.
Alle andere punten zijn ook zesmaal hoekpunt van een driehoek.
We krijgen zo in totaal 6 . 8 of 48 hoekpunten van driehoeken;
dat geeft 48 / 3 of 16 verschillende driehoeken.
Ik vernoemde lotte nog niet met haar antwoord.
Dus doe ik het nu: proficiat lotte - helemaal juist.
Oh ja, bijna vergeten:
- vraag 9 - sloeberkebebo - ok
- vraag 1 - lotte - ok
Voor iedereen, we zijn weer rond ...
tot maandag en dinsdag,
denook - een beetje 'ziekskes'
wat een problemen met die simpele achthoek en de driehoeken.
Het is onbegonnen werk om ze allemaal te willen tekenen - zou zeer
verwarrend zijn.
Belangrijk voor men start: in ieder van de acht hoekpunten moeten
evenveel driehoeken een hoekpunt hebben.
Zo kan het niet pastoor dat bij jou in punt 1, drie driehoeken komen
en in punt 6 komen er vijf toe.
Sloeberkebebo, eenzelfde diagonaal kan toch zijde zijn van meerdere
driehoeken!
Starten we met de nummering van pastoor; hoekpunten 1, 2, ... tot 8.
We tekenen alle driehoeken waar punt 1 een hoekpunt van is:
(1, 3, 5), (1, 3, 6), (1, 3, 7), (1, 4, 6), (1, 4, 7) en (1, 5, 7).
Dat zijn ze allemaal, zes in totaal.
Alle andere punten zijn ook zesmaal hoekpunt van een driehoek.
We krijgen zo in totaal 6 . 8 of 48 hoekpunten van driehoeken;
dat geeft 48 / 3 of 16 verschillende driehoeken.
Ik vernoemde lotte nog niet met haar antwoord.
Dus doe ik het nu: proficiat lotte - helemaal juist.
Oh ja, bijna vergeten:
- vraag 9 - sloeberkebebo - ok
- vraag 1 - lotte - ok
Voor iedereen, we zijn weer rond ...
tot maandag en dinsdag,
denook - een beetje 'ziekskes'
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Toch even een verklaring.
Dit kan wel: Zo kan het niet pastoor dat bij jou in punt 1, drie driehoeken komen en in punt 6 komen er vijf toe.
2. 1-4-6. dit wil zeggen van 1 naar 4 naar 6 en terug naar 1.
4. 2–4-6. dit wil zeggen van 2 naar 4 naar 6 en terug naar 2.
6. 2–6–8.
8. 3-6-8.
9. 4-6-8. dit wil zeggen van 4 naar 6 naar 8 en terug naar 4.
De lijn 4-6 is dezelfde ene lijn in de 3 gevallen.
Maar na 3 jaren kan ik nog altijd niet een tekening van de PC naar het seniorennet brengen (en dan was het begrijpbaar wat ik bedoelde).
Er zijn inderdaad 16 driehoeken met diagonalen, maar als men er 11 gemaakt heeft zijn alle mogelijke diagonalen reeds gebruikt. En de 5 andere driehoeken zijn duplicaten, die driehoeken staan er al en zijn niet nieuw. En dat was mijn uitgangspunt, wiskundig verkeerd, maar logisch juist. Mijn fout.
Dit kan wel: Zo kan het niet pastoor dat bij jou in punt 1, drie driehoeken komen en in punt 6 komen er vijf toe.
2. 1-4-6. dit wil zeggen van 1 naar 4 naar 6 en terug naar 1.
4. 2–4-6. dit wil zeggen van 2 naar 4 naar 6 en terug naar 2.
6. 2–6–8.
8. 3-6-8.
9. 4-6-8. dit wil zeggen van 4 naar 6 naar 8 en terug naar 4.
De lijn 4-6 is dezelfde ene lijn in de 3 gevallen.
Maar na 3 jaren kan ik nog altijd niet een tekening van de PC naar het seniorennet brengen (en dan was het begrijpbaar wat ik bedoelde).
Er zijn inderdaad 16 driehoeken met diagonalen, maar als men er 11 gemaakt heeft zijn alle mogelijke diagonalen reeds gebruikt. En de 5 andere driehoeken zijn duplicaten, die driehoeken staan er al en zijn niet nieuw. En dat was mijn uitgangspunt, wiskundig verkeerd, maar logisch juist. Mijn fout.
Sudoku, wijntjes proeven, genieten.
-
oomski - Lid geworden op: 28 mei 2008, 08:25
- Locatie: Thuis.
Hallo iedereen. Ik zie dat het mooie oefeningen waren, maar ik was met manlief enkele dagen op stap en heb dus niet kunnen meedoen  . Proficiat klasgenootjes voor de oplossingen en ... voor onze meester....vlugge beterschap.
. Proficiat klasgenootjes voor de oplossingen en ... voor onze meester....vlugge beterschap.
Wie op wraak zint, houdt zijn eigen wonden open.
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Lotte,
Eigenlijk niet, maar in de eerste "foutieve" oplossing van vraag 5, heb ik erbij geschreven dat duplicaten niet tellen, en vermits niemand daarop reageerde ben ik daarbij gebleven.
Alhoewel de duplicaten voor de zevenhoek er wel bij waren.
Eigenlijk niet, maar in de eerste "foutieve" oplossing van vraag 5, heb ik erbij geschreven dat duplicaten niet tellen, en vermits niemand daarop reageerde ben ik daarbij gebleven.
Alhoewel de duplicaten voor de zevenhoek er wel bij waren.
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste pastoor en iedereen die wil volgen ...
betreft onze achthoek van vraag 5.
Als we de hoekpunten 1, 2, 3, ... ,8 noemen
en we tekenen alle diaogonalen,
en we zoeken naar alle driehoeken, gevormd door die diagonalen,
dan krijgen we volgende 16 VERSCHILLENDE driehoeken
(1, 3, 5), (1, 3, 6), (1, 3, 7), (1, 4, 6), (1, 4, 7), (1, 5, 7)
(2, 4, 6), (2, 4, 7), (2, 4, 8 ), (2, 5, 7), (2, 5, 8 ), (2, 6, 8 )
(3, 5, 7), (3, 5, 8 ), (3, 6, 8 )
(4, 6, 8 ).
Dit zijn zoals reeds gezegd allemaal VERSCHILLENDE driehoeken;
hier is geen sprake van duplicaten.
Natuurlijk komen zijden van de ene driehoek ook in een andere
driehoek voor.
Zo heeft onze laatste driehoek (4, 6, 8 ),
een zijde (4-6) in driehoek (1, 4, 6),
een zijde (4-8 ) in driehoek (2, 4, 8 ) en
een zijde (6-8 ) in driehoek (2, 6, 8 );
maar (4, 6, 8 ) is een andere driehoek.
Als men goed kijkt ziet men dat elk hoekpunt precies 'zesmaal'
voorkomt. Dat moet ook want geen hoekpunt is beter of slechter dan
een ander.
groetjes,
denook
betreft onze achthoek van vraag 5.
Als we de hoekpunten 1, 2, 3, ... ,8 noemen
en we tekenen alle diaogonalen,
en we zoeken naar alle driehoeken, gevormd door die diagonalen,
dan krijgen we volgende 16 VERSCHILLENDE driehoeken
(1, 3, 5), (1, 3, 6), (1, 3, 7), (1, 4, 6), (1, 4, 7), (1, 5, 7)
(2, 4, 6), (2, 4, 7), (2, 4, 8 ), (2, 5, 7), (2, 5, 8 ), (2, 6, 8 )
(3, 5, 7), (3, 5, 8 ), (3, 6, 8 )
(4, 6, 8 ).
Dit zijn zoals reeds gezegd allemaal VERSCHILLENDE driehoeken;
hier is geen sprake van duplicaten.
Natuurlijk komen zijden van de ene driehoek ook in een andere
driehoek voor.
Zo heeft onze laatste driehoek (4, 6, 8 ),
een zijde (4-6) in driehoek (1, 4, 6),
een zijde (4-8 ) in driehoek (2, 4, 8 ) en
een zijde (6-8 ) in driehoek (2, 6, 8 );
maar (4, 6, 8 ) is een andere driehoek.
Als men goed kijkt ziet men dat elk hoekpunt precies 'zesmaal'
voorkomt. Dat moet ook want geen hoekpunt is beter of slechter dan
een ander.
groetjes,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste leerlingen,
hier de oplossingen van de vorige les over getallen.
1) (3 - 7i).(3 + 7i) = 9 + 21i - 21i - 49i² = 9 + 49 = 58
2) (5 -2i) / (6 - 3i) = (5-2i).(6+3i) / (6-3i).(6+3i)
= (30 + 15i - 12i - 6i²) / (36 + 9)
= (30 + 3i + 6) / 45
= (36 + 3i) / 45 = 36/45 + 3i/45 = 4/5 + i/15
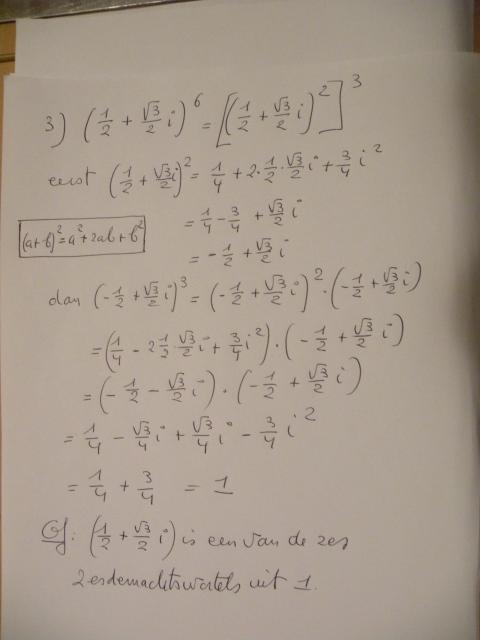
tot morgen,
denook
hier de oplossingen van de vorige les over getallen.
1) (3 - 7i).(3 + 7i) = 9 + 21i - 21i - 49i² = 9 + 49 = 58
2) (5 -2i) / (6 - 3i) = (5-2i).(6+3i) / (6-3i).(6+3i)
= (30 + 15i - 12i - 6i²) / (36 + 9)
= (30 + 3i + 6) / 45
= (36 + 3i) / 45 = 36/45 + 3i/45 = 4/5 + i/15
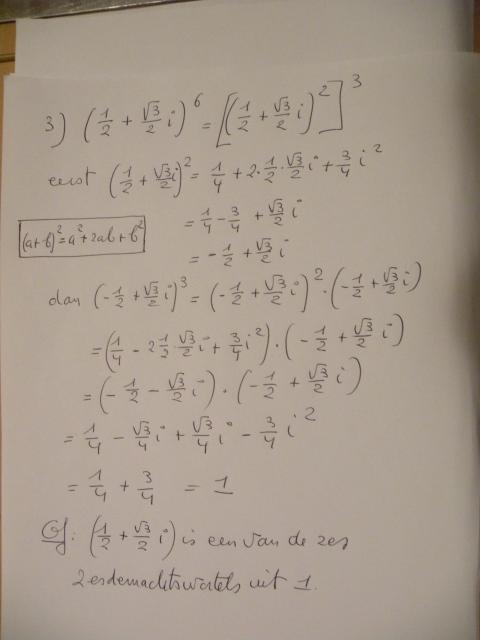
tot morgen,
denook