Wiskundige problemen en probleempjes 2
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Met de groeten van meester Denook
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
nog meer getallen - (voorlopig) einde
Alles nog eens op een rijtje.
Hieronder de verzameling R van de reële getallen
en alle deelverzamelingen ervan.
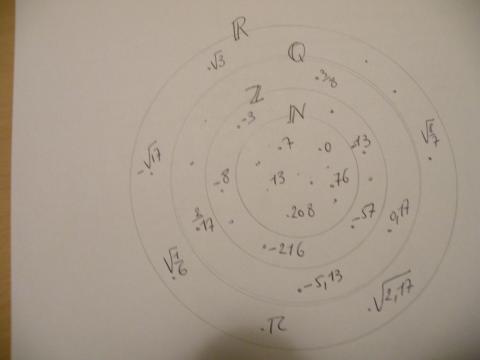
Dan een voorstelling van de complexe getallen waarvan dan weer
de reële getallen en de imaginaire getallen deelverzamelingen zijn.
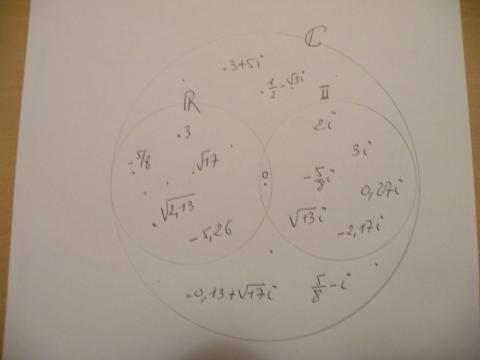
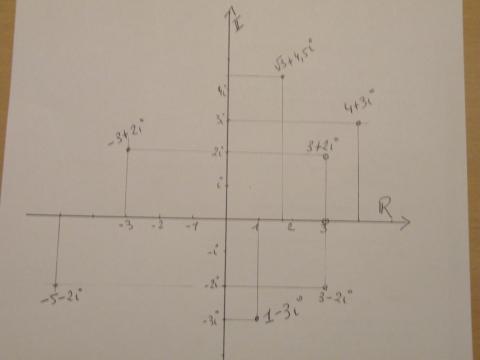
Tenslotte stellen we "ALLE" getallen voor in een loodrecht assenstelsel.
Op de X-as komen ALLE reële getallen.
Op de Y-as komen ALLE imaginaire getallen.
Ieder puntje in het vlak dat niet op een van de assen ligt stelt dan een
complex getal voor dat noch reëel, noch imaginair is.
Merk ook op hoe het 'gemiddelde' van twee 'toegevoegd complexe
getallen' steeds reëel is .
( op de figuur: gemiddelde van 3+2i en 3-2i is 3)
Weet je nog onze vierkantsvergelijking ax² + bx + c = 0.
Deze vergelijking kon GEEN, EEN of TWEE oplossingen hebben.
Dat was zo als we in R werkten.
Nu zeggen we: iedere vierkantsvergelijking heeft STEEDS TWEE
oplossingen.
Deze kunnen:
- reëel en verschillend zijn,
- reëel en samenvallend zijn,
- imaginair en toegevoegd zijn.
voorbeelden:
2x² + 7x - 15 = 0; oplossingen: x1 = -5 en x2 = 3/2
4x² - 20x + 25 = 0; oplossingen: x1 = x2 = 5/2
x² - 2x + 10 = 0; oplossingen: x1 = 1 + 3i en x2 = 1 - 3i
reken maar na met de formule x1 = (-b+wortel(b²-4ac))/2a
en x2 = (-b - wortel(b²-4ac))/2a
nog drie oefeningen voor thuis
los op:
1) -9x² + 12x - 4 = O
2) x² -6x + 10 = 0
3) -6x² - 11x + 10 = 0
groetjes, denook
opm. ieder complex getal heeft ook een vierkantswortel.
Zo is de wortel uit (5 - 12i) gelijk aan (3 - 2i). Reken maar na.
Ook daar bestaan weer formules voor.
Alles nog eens op een rijtje.
Hieronder de verzameling R van de reële getallen
en alle deelverzamelingen ervan.

Dan een voorstelling van de complexe getallen waarvan dan weer
de reële getallen en de imaginaire getallen deelverzamelingen zijn.

Tenslotte stellen we "ALLE" getallen voor in een loodrecht assenstelsel.
Op de X-as komen ALLE reële getallen.
Op de Y-as komen ALLE imaginaire getallen.
Ieder puntje in het vlak dat niet op een van de assen ligt stelt dan een
complex getal voor dat noch reëel, noch imaginair is.
Merk ook op hoe het 'gemiddelde' van twee 'toegevoegd complexe
getallen' steeds reëel is .
( op de figuur: gemiddelde van 3+2i en 3-2i is 3)

Weet je nog onze vierkantsvergelijking ax² + bx + c = 0.
Deze vergelijking kon GEEN, EEN of TWEE oplossingen hebben.
Dat was zo als we in R werkten.
Nu zeggen we: iedere vierkantsvergelijking heeft STEEDS TWEE
oplossingen.
Deze kunnen:
- reëel en verschillend zijn,
- reëel en samenvallend zijn,
- imaginair en toegevoegd zijn.
voorbeelden:
2x² + 7x - 15 = 0; oplossingen: x1 = -5 en x2 = 3/2
4x² - 20x + 25 = 0; oplossingen: x1 = x2 = 5/2
x² - 2x + 10 = 0; oplossingen: x1 = 1 + 3i en x2 = 1 - 3i
reken maar na met de formule x1 = (-b+wortel(b²-4ac))/2a
en x2 = (-b - wortel(b²-4ac))/2a
nog drie oefeningen voor thuis
los op:
1) -9x² + 12x - 4 = O
2) x² -6x + 10 = 0
3) -6x² - 11x + 10 = 0
groetjes, denook
opm. ieder complex getal heeft ook een vierkantswortel.
Zo is de wortel uit (5 - 12i) gelijk aan (3 - 2i). Reken maar na.
Ook daar bestaan weer formules voor.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
morgen, morgen, morgen ...
nieuwe reeks probleempjes en problemen.
Waarom dit kort bericht?
Ik vraag me af of er wel leerlingen zijn die ook de veertiendaagse
lessen een beetje volgen. Morgen zijn er twee vraagjes bij die echt
refereren naar vroegere lessen.
Voor diegenen die het wat bijhielden: er is een vraag bij die handelt
over REKENKUNDIGE RIJEN en een andere gaat over oplossen van een
VIERKANTSVERGELIJKING. Blader maar eens terug.
Voor de rest een mooie mix van 'voor ieder wat wils',
tot morgen,
denook
nieuwe reeks probleempjes en problemen.
Waarom dit kort bericht?
Ik vraag me af of er wel leerlingen zijn die ook de veertiendaagse
lessen een beetje volgen. Morgen zijn er twee vraagjes bij die echt
refereren naar vroegere lessen.
Voor diegenen die het wat bijhielden: er is een vraag bij die handelt
over REKENKUNDIGE RIJEN en een andere gaat over oplossen van een
VIERKANTSVERGELIJKING. Blader maar eens terug.
Voor de rest een mooie mix van 'voor ieder wat wils',
tot morgen,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
Dinsdag 8 december – wiskundige problemen en probleempjes,
1. Vijf bakjes staan naast elkaar en zijn genummerd a, b, c, d en e, in die volgorde. Een slimme hond neemt uit een grote mand telkens twee balletjes en legt die in twee aan elkaar grenzende bakjes. Na een tijdje liggen in bakje a twee balletjes, in bakje b drie balletjes, in bakje c vier balletjes en in bakje d vijf balletjes. Hoeveel balletjes liggen in bakje e?
3. Een getal bestaat uit zeven cijfers.
Het eerste cijfers geeft het aantal nullen in het getal,
het tweede cijfer geeft het aantal enen in het getal,
het derde cijfer geeft het aantal tweeën in het getal,
……..
het zevende cijfer geeft het aantal zessen in het getal.
Tracht het getal te schrijven ….. (puzzelwerk)
4. Door de cijfers 2, 3, 4, 6, 7, 8 telkens éénmaal te gebruiken schrijven we twee getallen van drie cijfers. De getallen moeten zo geschreven worden dat hun verschil zo klein mogelijk is.
Wat is het kleinst mogelijke verschil?
5. Als 4 . ( 7 . (5 + 6) . 8 + 9 – x) = 2008, dan is x = ???
6. a²x² + ax + 2 = 0 is een vierkantsvergelijking in x, met a een willekeurig getal, verschillend van nul.
Wat weet je over het aantal oplossingen van deze vergelijking?
A) nooit een oplossing,
B) altijd één oplossing,
C) altijd precies twee oplossingen
D) aantal oplossingen hangt af van de waarde van a.
7. Als 6/9, 10/35, 16/20, 8/12, 4/14, 12/n, zes breuken zijn met drie verschillende waarden en elke waarde komt tweemaal voor, wat is dan het getal n?
8. Van een rekenkundige rij is de som van de eerste n termen steeds gelijk aan 2n² + 3n, voor iedere waarde van n.
Bepaal de derde term van deze rij.
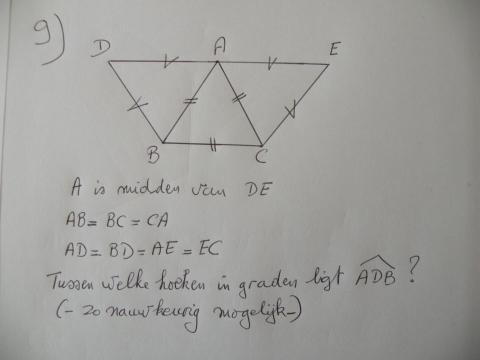
10. Als n een geheel getal is, verschillend van nul, hoeveel gehele getallen liggen er dan tussen -n en n ?
veel succes –
nieuwe leerlingen steeds welkom;
deze lezen wel eerst blz 1.
Tot morgen, denook
1. Vijf bakjes staan naast elkaar en zijn genummerd a, b, c, d en e, in die volgorde. Een slimme hond neemt uit een grote mand telkens twee balletjes en legt die in twee aan elkaar grenzende bakjes. Na een tijdje liggen in bakje a twee balletjes, in bakje b drie balletjes, in bakje c vier balletjes en in bakje d vijf balletjes. Hoeveel balletjes liggen in bakje e?

3. Een getal bestaat uit zeven cijfers.
Het eerste cijfers geeft het aantal nullen in het getal,
het tweede cijfer geeft het aantal enen in het getal,
het derde cijfer geeft het aantal tweeën in het getal,
……..
het zevende cijfer geeft het aantal zessen in het getal.
Tracht het getal te schrijven ….. (puzzelwerk)
4. Door de cijfers 2, 3, 4, 6, 7, 8 telkens éénmaal te gebruiken schrijven we twee getallen van drie cijfers. De getallen moeten zo geschreven worden dat hun verschil zo klein mogelijk is.
Wat is het kleinst mogelijke verschil?
5. Als 4 . ( 7 . (5 + 6) . 8 + 9 – x) = 2008, dan is x = ???
6. a²x² + ax + 2 = 0 is een vierkantsvergelijking in x, met a een willekeurig getal, verschillend van nul.
Wat weet je over het aantal oplossingen van deze vergelijking?
A) nooit een oplossing,
B) altijd één oplossing,
C) altijd precies twee oplossingen
D) aantal oplossingen hangt af van de waarde van a.
7. Als 6/9, 10/35, 16/20, 8/12, 4/14, 12/n, zes breuken zijn met drie verschillende waarden en elke waarde komt tweemaal voor, wat is dan het getal n?
8. Van een rekenkundige rij is de som van de eerste n termen steeds gelijk aan 2n² + 3n, voor iedere waarde van n.
Bepaal de derde term van deze rij.

10. Als n een geheel getal is, verschillend van nul, hoeveel gehele getallen liggen er dan tussen -n en n ?
veel succes –
nieuwe leerlingen steeds welkom;
deze lezen wel eerst blz 1.
Tot morgen, denook
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Goede avond Denook en allemaal.
Vraag 1. Vijf bakjes staan naast elkaar en zijn genummerd a, b, c, d en e, in die volgorde. Een slimme hond neemt uit een grote mand telkens twee balletjes en legt die in twee aan elkaar grenzende bakjes. Na een tijdje liggen in bakje a twee balletjes, in bakje b drie balletjes, in bakje c vier balletjes en in bakje d vijf balletjes. Hoeveel balletjes liggen in bakje e?
Er liggen 2 balletjes in vakje e. (denk ik)
Vraag 1. Vijf bakjes staan naast elkaar en zijn genummerd a, b, c, d en e, in die volgorde. Een slimme hond neemt uit een grote mand telkens twee balletjes en legt die in twee aan elkaar grenzende bakjes. Na een tijdje liggen in bakje a twee balletjes, in bakje b drie balletjes, in bakje c vier balletjes en in bakje d vijf balletjes. Hoeveel balletjes liggen in bakje e?
Er liggen 2 balletjes in vakje e. (denk ik)
Laatst gewijzigd door pastoor op 08 dec 2009, 21:08, 1 keer totaal gewijzigd.
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goeden avond allemaal
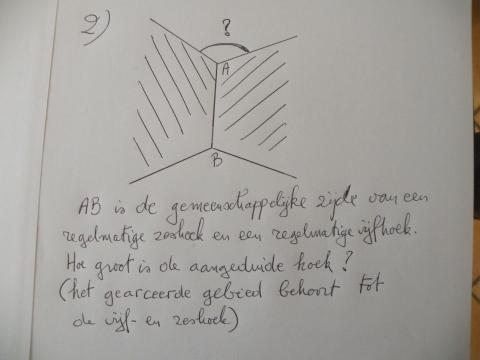
Vraag 2
360° - ( 120°+108°) = 132°
De hoek is 132°
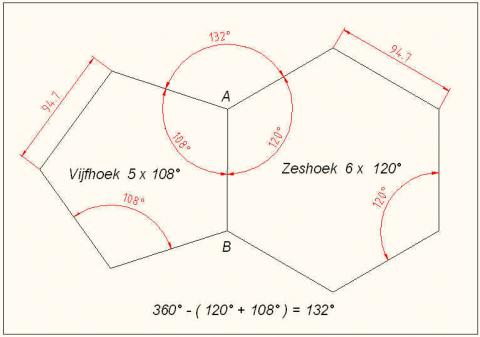
Groetjes
Sloeber
Vraag 2
360° - ( 120°+108°) = 132°
De hoek is 132°

Groetjes
Sloeber
Laatst gewijzigd door sloeberkebebo op 08 dec 2009, 21:57, 1 keer totaal gewijzigd.
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Chérie,
Als er in de bakjes a, b, c, en d al 2, 3, 4 en 5 balletjes liggen, dan is de som gelijk aan 14, een even getal. En vermits het slimme hondje telkens twee balletjes neemt, moet het aantal even zijn, dus 16 en niet 15, of 2 balletjes in bakje e.
Als er in de bakjes a, b, c, en d al 2, 3, 4 en 5 balletjes liggen, dan is de som gelijk aan 14, een even getal. En vermits het slimme hondje telkens twee balletjes neemt, moet het aantal even zijn, dus 16 en niet 15, of 2 balletjes in bakje e.
Laatst gewijzigd door pastoor op 08 dec 2009, 23:24, 1 keer totaal gewijzigd.
Sudoku, wijntjes proeven, genieten.