Wiskundige problemen en probleempjes 2
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
eerste evaluatie
vraag 1) pastoor - ok - ook chérie en lotte
even proberen, zoals waarschijnlijk ook chérie deed
vak a : 2 ballen, dus ook vak b : 2 ballen,
maar in b liggen er 3, dus
1 bal ervan ook in c,
maar in c liggen er 4, dus
3 ballen ervan ook in d,
maar in d liggen er 5, dus
2 ballen ervan ook in e.
vraag 7) lotte - ok
vraag 2) sloeberkebebo - ok - natuurlijk, en mooie tekening
vraag 4) troontje - neen, denk ik ...
(van welke twee getallen is het verschil 39? - ik vind er geen)
voorbeeld: 673 - 284 = 389
die 389 moet omlaag!!
voorbeeld 346 - 287 = 59 vond pastoor ook.
ken jij twee getallen troontje waarvan het verschil nog kleiner is?
we zijn rond,
tot morgen?
denook
Oh ja, mag ik de aanwezigheid van chérie toejuichen.
Ik sta vol bewondering voor haar taalkennis
(- zie andere spelletjes waar ze dikwijls vlug en accuraat de
anderen voor is - kan ik niet aan tippen - en zo heeft iedereen
een specialiteit-).
vraag 1) pastoor - ok - ook chérie en lotte
even proberen, zoals waarschijnlijk ook chérie deed
vak a : 2 ballen, dus ook vak b : 2 ballen,
maar in b liggen er 3, dus
1 bal ervan ook in c,
maar in c liggen er 4, dus
3 ballen ervan ook in d,
maar in d liggen er 5, dus
2 ballen ervan ook in e.
vraag 7) lotte - ok
vraag 2) sloeberkebebo - ok - natuurlijk, en mooie tekening
vraag 4) troontje - neen, denk ik ...
(van welke twee getallen is het verschil 39? - ik vind er geen)
voorbeeld: 673 - 284 = 389
die 389 moet omlaag!!
voorbeeld 346 - 287 = 59 vond pastoor ook.
ken jij twee getallen troontje waarvan het verschil nog kleiner is?
we zijn rond,
tot morgen?
denook
Oh ja, mag ik de aanwezigheid van chérie toejuichen.
Ik sta vol bewondering voor haar taalkennis
(- zie andere spelletjes waar ze dikwijls vlug en accuraat de
anderen voor is - kan ik niet aan tippen - en zo heeft iedereen
een specialiteit-).
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Vraag 8. Van een rekenkundige rij is de som van de eerste n termen steeds gelijk aan 2n² + 3n, voor iedere waarde van n. Bepaal de derde term van deze rij.
Eerste term, de som van een term is: 2.1² + 3.1 = 5.
De eerste term is 5.
Twee termen, de som van twee termen is: 2.2² + 3.2 = 14.
De eerste term was 5. De tweede term is 14 - 5 = 9.
Drie termen, de som van drie termen is: 2.3² + 3.3 = 27.
De som van twee termen was 14. De derde term is 27 – 14 = 13.
De rij is 5 – 9 – 13 – 17 – 21
Antwoord: de derde term van deze rij is 13
Eerste term, de som van een term is: 2.1² + 3.1 = 5.
De eerste term is 5.
Twee termen, de som van twee termen is: 2.2² + 3.2 = 14.
De eerste term was 5. De tweede term is 14 - 5 = 9.
Drie termen, de som van drie termen is: 2.3² + 3.3 = 27.
De som van twee termen was 14. De derde term is 27 – 14 = 13.
De rij is 5 – 9 – 13 – 17 – 21
Antwoord: de derde term van deze rij is 13
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goeden avond allemaal
Vraag 9
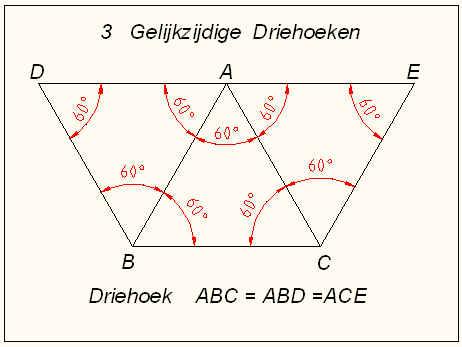
Groetjes
Sloeber
Vraag 9

Groetjes
Sloeber
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond beste leerlingen,
vervolg evaluatie
vraag 8. pastoor - ok - mooi ook
vraag 3. lotte - ok - ook mooi gepuzzeld
vraag 9. sloeverkebebo - ok - en weer mooi getekend
hier was de vraag (-strikvraag eigenlijk-):
tussen welke hoeken, in graden, ligt de hoek ADB - zo nauwkeurig
mogelijk.
de hoek was 'precies' 60°; voor sloeberkebebo geen probleem.
en dan was er nog vraag 4 - troontje - OK, OK, OK ...
daar staan we dan hé pastoor
blijven over: 5, 6 en 10,
tegen morgen is dat allemaal opgelost,
voel ik zo,
tot dan,
denook
vervolg evaluatie
vraag 8. pastoor - ok - mooi ook
vraag 3. lotte - ok - ook mooi gepuzzeld
vraag 9. sloeverkebebo - ok - en weer mooi getekend
hier was de vraag (-strikvraag eigenlijk-):
tussen welke hoeken, in graden, ligt de hoek ADB - zo nauwkeurig
mogelijk.
de hoek was 'precies' 60°; voor sloeberkebebo geen probleem.
en dan was er nog vraag 4 - troontje - OK, OK, OK ...
daar staan we dan hé pastoor
blijven over: 5, 6 en 10,
tegen morgen is dat allemaal opgelost,
voel ik zo,
tot dan,
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goeden avond allemaal
Beste Troontje , ge moet niet twijfelen : ' t is just !
(7*(5+6)* 8 )+9=625
2008/4=502
625-502=123=x
Groetjes
Sloeber
Beste Troontje , ge moet niet twijfelen : ' t is just !
(7*(5+6)* 8 )+9=625
2008/4=502
625-502=123=x
Groetjes
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Goede avond Denook en allemaal.
Vraag 6.
a²x² + ax + 2 = 0 is een vierkantsvergelijking in x, met a een willekeurig getal, verschillend van nul. Wat weet je over het aantal oplossingen van deze vergelijking? A) nooit een oplossing. B) altijd één oplossing. C) altijd precies twee oplossingen. D) aantal oplossingen hangt af van de waarde van a.
Bepalen van de discriminant (D = B² - 4AC).
D = a² - 4.a².2 = a² - 8a² = -7a² De discriminant is hier altijd negatief.
Er is geen oplossing in de verzameling R.
* * * * *
Is er een oplossing in de verzameling C?
Discriminant D = -7a² = 7a²i² of √D = i.a.√7.
Dat levert twee oplossingen:
Oplossing: X1 = (-a + i.a.√7)/2a² = (i.√7 - 1)/2a = ((√-1).(√7) - 1)/2a
Oplossing: X2 = (-a – i.a.√7)/2a² = (-i.√7 - 1)/2a = (-(√-1).(√7) -1)/2a
Nazien met
X1 = ((√-1).(√7) - 1)/2a en de vergelijking (a²x² + ax + 2 = 0)
Of a²((-(√-1).(√7) -1)/2a)² + a((-(√-1).(√7) -1)/2a) + 2 = 0
Of ((-(√-1).(√7) + (-1))/2)² + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-(√-1).(√7)) + (-1))²/2² + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-(√-1).(√7))²+(-1)² 2(-1)(-(√-1).(√7)))/4 + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-1).(7) + (1) + 2(√-1).(√7))/4 + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-7) + (1) + 2(√-1).(√7)) + (-(√-1).(√7) -1).2 + 8 = 0
Of -7 + 1 + 2(√-1).(√7) -2(√-1).(√7) -2 + 8 = 0
Of 2(√-1).(√7) -2(√-1).(√7) = 0
Nazien met
X2 = (-(√-1).(√7) - 1)/2a en de vergelijking (a²x² + ax + 2 = 0)
Of a²(-(√-1).(√7) - 1)²/(2a)² + a(-(√-1).(√7) - 1)/2a + 2 = 0
Of (-(√-1).(√7) - 1)²/2² + (-(√-1).(√7) - 1)/2 + 2 = 0
Of ((-1).(7) + 2(√-1).(√7) + 1)/4 + (-(√-1).(√7) - 1)/2 + 2 = 0
Of ((-7) + 2(√-1).(√7) + 1)/4 + (-(√-1).(√7) - 1)/2 + 2 = 0
Of ((-7) + 2(√-1).(√7) + 1) + (-(√-1).(√7) - 1)2 + 8 = 0
Of -7 + 2(√-1).(√7) + 1 + - 2(√-1).(√7) - 2 + 8 = 0
Of 2(√-1).(√7) - 2(√-1).(√7) = 0
Met complexe getallen zijn er twee oplossingen in verzameling C:
X1 = ((√-1).(√7) - 1)/2a en X2 = (-(√-1).(√7) -1)/2a
* * * * *
Antwoord: voor die vergelijking is er nooit een oplossing in de verzameling R, maar zijn er altijd precies twee oplossingen in de verzameling C. Dus antwoord A en C.
Vraag 6.
a²x² + ax + 2 = 0 is een vierkantsvergelijking in x, met a een willekeurig getal, verschillend van nul. Wat weet je over het aantal oplossingen van deze vergelijking? A) nooit een oplossing. B) altijd één oplossing. C) altijd precies twee oplossingen. D) aantal oplossingen hangt af van de waarde van a.
Bepalen van de discriminant (D = B² - 4AC).
D = a² - 4.a².2 = a² - 8a² = -7a² De discriminant is hier altijd negatief.
Er is geen oplossing in de verzameling R.
* * * * *
Is er een oplossing in de verzameling C?
Discriminant D = -7a² = 7a²i² of √D = i.a.√7.
Dat levert twee oplossingen:
Oplossing: X1 = (-a + i.a.√7)/2a² = (i.√7 - 1)/2a = ((√-1).(√7) - 1)/2a
Oplossing: X2 = (-a – i.a.√7)/2a² = (-i.√7 - 1)/2a = (-(√-1).(√7) -1)/2a
Nazien met
X1 = ((√-1).(√7) - 1)/2a en de vergelijking (a²x² + ax + 2 = 0)
Of a²((-(√-1).(√7) -1)/2a)² + a((-(√-1).(√7) -1)/2a) + 2 = 0
Of ((-(√-1).(√7) + (-1))/2)² + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-(√-1).(√7)) + (-1))²/2² + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-(√-1).(√7))²+(-1)² 2(-1)(-(√-1).(√7)))/4 + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-1).(7) + (1) + 2(√-1).(√7))/4 + (-(√-1).(√7) -1)/2 + 2 = 0
Of ((-7) + (1) + 2(√-1).(√7)) + (-(√-1).(√7) -1).2 + 8 = 0
Of -7 + 1 + 2(√-1).(√7) -2(√-1).(√7) -2 + 8 = 0
Of 2(√-1).(√7) -2(√-1).(√7) = 0
Nazien met
X2 = (-(√-1).(√7) - 1)/2a en de vergelijking (a²x² + ax + 2 = 0)
Of a²(-(√-1).(√7) - 1)²/(2a)² + a(-(√-1).(√7) - 1)/2a + 2 = 0
Of (-(√-1).(√7) - 1)²/2² + (-(√-1).(√7) - 1)/2 + 2 = 0
Of ((-1).(7) + 2(√-1).(√7) + 1)/4 + (-(√-1).(√7) - 1)/2 + 2 = 0
Of ((-7) + 2(√-1).(√7) + 1)/4 + (-(√-1).(√7) - 1)/2 + 2 = 0
Of ((-7) + 2(√-1).(√7) + 1) + (-(√-1).(√7) - 1)2 + 8 = 0
Of -7 + 2(√-1).(√7) + 1 + - 2(√-1).(√7) - 2 + 8 = 0
Of 2(√-1).(√7) - 2(√-1).(√7) = 0
Met complexe getallen zijn er twee oplossingen in verzameling C:
X1 = ((√-1).(√7) - 1)/2a en X2 = (-(√-1).(√7) -1)/2a
* * * * *
Antwoord: voor die vergelijking is er nooit een oplossing in de verzameling R, maar zijn er altijd precies twee oplossingen in de verzameling C. Dus antwoord A en C.
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste leerlingen,
we gaan niet wachten tot morgen -
het is weer geklaard, en hoe ...
vraag 5. - troontje - ok
je hoeft geen '?' te plaatsen,
het is ok - mooi uitgewerkt,
ook sloeberkebebo en lotte beamen nadien
vraag 6 - pastoor - ok
lieve pastoor, prachtig gewerkt, maar ...
in 't vervolg, als er niks expliciet bijstaat,
werken we altijd in R.
Trouwens in C heeft elke vierkantsvergelijking
twee oplossingen
vraag 10 - lotte - ok
Waar zit oomski nu weer -
nog eens op reis ...
er waren nochthans bewust een paar vragen
naar haar smaak ingeslopen.
Proficiat allemaal,
tot woensdag voor een lesje,
volgende problemen op 22 december
(- uitzonderlijk toch eens tijdens het schoolverlof-)
tot dan,
denook
we gaan niet wachten tot morgen -
het is weer geklaard, en hoe ...
vraag 5. - troontje - ok
je hoeft geen '?' te plaatsen,
het is ok - mooi uitgewerkt,
ook sloeberkebebo en lotte beamen nadien
vraag 6 - pastoor - ok
lieve pastoor, prachtig gewerkt, maar ...
in 't vervolg, als er niks expliciet bijstaat,
werken we altijd in R.
Trouwens in C heeft elke vierkantsvergelijking
twee oplossingen
vraag 10 - lotte - ok
Waar zit oomski nu weer -
nog eens op reis ...
er waren nochthans bewust een paar vragen
naar haar smaak ingeslopen.
Proficiat allemaal,
tot woensdag voor een lesje,
volgende problemen op 22 december
(- uitzonderlijk toch eens tijdens het schoolverlof-)
tot dan,
denook
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Gevonden in Wikipedia.
http://nl.wikipedia.org/wiki/Autobiografisch_getal
1210
2020
21200
3211000 <------
42101000
521001000
6210001000
(Selfdescripting-numbers).
http://nl.wikipedia.org/wiki/Autobiografisch_getal
1210
2020
21200
3211000 <------
42101000
521001000
6210001000
(Selfdescripting-numbers).
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
hallo iedereen,
bijna vergeten ... oplossingen oefeningen van di 1 december
1) -9x² + 12x - 4 = 0
Discriminant: D = b² - 4ac = 12² - 4.(-9).(-4) = 144 - 144 = 0 !!!
oplossing: (-b + wortelD) / 2a = (-12 + 0) / -18 = 12/18 = 2/3
en (-b - wortelD) / 2a = ... = 2/3
2) x² - 6x + 10 = 0
discriminant: D = b² - 4ac = (-6)² - 4.1.10 = 36 - 40 = -4
oplossing: (-b + wortelD) / 2a = (6 + wortel(-4)) / 2 = (6+2i)/2 = 3 + i
en (-b - wortelD) / 2a = ... 3 - i
3) -6x² - 11x + 10 = 0
discriminant: D = b² - 4ac = (-11)² - 4.(-6).10 = 121 + 240 = 361
oplossing: (-b + wortelD) / 2a = (11 + 19) / (-12) = 30/(-12) = -5/2
en (-b - wortelD) / 2a = .... = (11 - 19) / (-12) = -8/-12 = 2/3
tot morgen, voor iets nieuws,
eigenlijk iets heel ouds,
dat iedereen zich zal herinneren ...
of toch ongeveer,
denook
bijna vergeten ... oplossingen oefeningen van di 1 december
1) -9x² + 12x - 4 = 0
Discriminant: D = b² - 4ac = 12² - 4.(-9).(-4) = 144 - 144 = 0 !!!
oplossing: (-b + wortelD) / 2a = (-12 + 0) / -18 = 12/18 = 2/3
en (-b - wortelD) / 2a = ... = 2/3
2) x² - 6x + 10 = 0
discriminant: D = b² - 4ac = (-6)² - 4.1.10 = 36 - 40 = -4
oplossing: (-b + wortelD) / 2a = (6 + wortel(-4)) / 2 = (6+2i)/2 = 3 + i
en (-b - wortelD) / 2a = ... 3 - i
3) -6x² - 11x + 10 = 0
discriminant: D = b² - 4ac = (-11)² - 4.(-6).10 = 121 + 240 = 361
oplossing: (-b + wortelD) / 2a = (11 + 19) / (-12) = 30/(-12) = -5/2
en (-b - wortelD) / 2a = .... = (11 - 19) / (-12) = -8/-12 = 2/3
tot morgen, voor iets nieuws,
eigenlijk iets heel ouds,
dat iedereen zich zal herinneren ...
of toch ongeveer,
denook