Wiskundige problemen en probleempjes 2
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
... meester denook,
voor vraag 4 heb ik veel getallen geprobeerd
ik voel dat het antwoord 'geen' is,
vind er wel geen bewijs voor.
mijn antwoord is dus: GEEN
en pastoor mag uitleggen waarom ik
gelijk of ongelijk heb.
groetjes aan iedereen,
lotte .
voor vraag 4 heb ik veel getallen geprobeerd
ik voel dat het antwoord 'geen' is,
vind er wel geen bewijs voor.
mijn antwoord is dus: GEEN
en pastoor mag uitleggen waarom ik
gelijk of ongelijk heb.
groetjes aan iedereen,
lotte .
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Gode avond allemaal.
Vraag 9.
A, B, C, D en E zijn vijf natuurlijke getallen waarvoor geldt dat: als je twee of drie naast elkaar liggende getallen optelt, is de som nooit een drievoud. Hoeveel van deze getallen zijn dan zelf wel een drievoud?
A)geen, B) een, C) twee, D) drie, E) kan niet bepaald worden
Stel: 3V is een drievoud, en N3V is geen drievoud.
Dan gelden de volgende regels.
3V + 3V = 3V (regel 1), niet goed.
3V + N3V = N3V (regel 2), goed.
N3V + N3V = kan een 3V zijn (regel 3), niet goed.
3V + 3V + 3V = 3V (regel 4), niet goed.
3V + 3V + N3V = N3V (5) mag niet volgens (regel 1), niet goed.
3V + N3V + 3V = N3V (regel 6), goed.
3V + N3V + N3V = kan een 3V zijn (regel 7), niet goed.
N3V + 3V + N3V = kan een 3V zijn (regel 8 ), niet goed.
N3V + N3V + N3V = kan een 3V zijn (regel 9), niet goed,
Alleen de (regel 2) en (regel 6) voldoen aan de opgave (leveren geen 3V).
Stel dat A=3V is.
Dan moet B=N3V zijn (regel2).
Dan moet C=3V zijn (dat voldoet aan regel (2) en regel (6)).
Als D=3V is, dan loopt het fout volgens regel (1).
Als D=N3V is, dan loopt het fout volgens regel ( 8 ).
Stel dat A=N3V.
Dan moet B= 3V (regel 2) en (regel 3).
Als C=3V is, dan loopt het fout volgens (regel 1).
Als C=N3V is, dan loopt het fout regel volgens (regel 8 ).
Antwoord: E, kan niet bepaald worden.
Vraag 9.
A, B, C, D en E zijn vijf natuurlijke getallen waarvoor geldt dat: als je twee of drie naast elkaar liggende getallen optelt, is de som nooit een drievoud. Hoeveel van deze getallen zijn dan zelf wel een drievoud?
A)geen, B) een, C) twee, D) drie, E) kan niet bepaald worden
Stel: 3V is een drievoud, en N3V is geen drievoud.
Dan gelden de volgende regels.
3V + 3V = 3V (regel 1), niet goed.
3V + N3V = N3V (regel 2), goed.
N3V + N3V = kan een 3V zijn (regel 3), niet goed.
3V + 3V + 3V = 3V (regel 4), niet goed.
3V + 3V + N3V = N3V (5) mag niet volgens (regel 1), niet goed.
3V + N3V + 3V = N3V (regel 6), goed.
3V + N3V + N3V = kan een 3V zijn (regel 7), niet goed.
N3V + 3V + N3V = kan een 3V zijn (regel 8 ), niet goed.
N3V + N3V + N3V = kan een 3V zijn (regel 9), niet goed,
Alleen de (regel 2) en (regel 6) voldoen aan de opgave (leveren geen 3V).
Stel dat A=3V is.
Dan moet B=N3V zijn (regel2).
Dan moet C=3V zijn (dat voldoet aan regel (2) en regel (6)).
Als D=3V is, dan loopt het fout volgens regel (1).
Als D=N3V is, dan loopt het fout volgens regel ( 8 ).
Stel dat A=N3V.
Dan moet B= 3V (regel 2) en (regel 3).
Als C=3V is, dan loopt het fout volgens (regel 1).
Als C=N3V is, dan loopt het fout regel volgens (regel 8 ).
Antwoord: E, kan niet bepaald worden.
Laatst gewijzigd door pastoor op 31 jan 2010, 10:58, 1 keer totaal gewijzigd.
Sudoku, wijntjes proeven, genieten.
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Vraag 4) Hoeveel drietallen positieve reële getallen a, b, en c zijn er waarvoor geldt: a.b.c = 1 én a + b + c = 1?
Oplossen van (a.b.c = 1) met substittie.
Stel a = x1/x2, b = x2/x3 en c= x3/x1.
Na substitutie in (a.b.c = 1), wordt dat (x1.x2.x3)/(x1.x2.x3) = 1.
Alle reële getallen kunnen gebruikt worden voor x1, x2 en x3.
Voorbeeld x1 = i, x2 = e (euler), x3 = π.
Er zijn oneindig oplossingen.
* * * * *
Oplossen van (a + b + c = 1) (1) met substitutie.
Stel: y1.y2 + y2.y3 + y3.y1 = 1 (2).
Deel (2) door (y1.y2.y3), dat wordt:
(y1.y2/y1.y2.y3) + (y2.y3/y1.y2.y3) + (y3.y1/y1.y2.y3) = (1/y1.y2.y3)
Vereenvoudigd: (1/y3) + (1/y1) + (1/y2) = (1/y1.y2.y3) (3)
Stel a = 1/y1, b = 1/y2, c = 1/y3 en die vervangen in vergelijking (3).
Dat wordt: a + b + c = a.b.c = 1
Vermits (a.b.c=1) oneindig oplosingen heeft, heeft (a+b+c=1) dat ook.
Er zijn oneindig oplossingen..
a + b + c = a.b.c = 1 heeft oneindig oplossingen.
Oplossen van (a.b.c = 1) met substittie.
Stel a = x1/x2, b = x2/x3 en c= x3/x1.
Na substitutie in (a.b.c = 1), wordt dat (x1.x2.x3)/(x1.x2.x3) = 1.
Alle reële getallen kunnen gebruikt worden voor x1, x2 en x3.
Voorbeeld x1 = i, x2 = e (euler), x3 = π.
Er zijn oneindig oplossingen.
* * * * *
Oplossen van (a + b + c = 1) (1) met substitutie.
Stel: y1.y2 + y2.y3 + y3.y1 = 1 (2).
Deel (2) door (y1.y2.y3), dat wordt:
(y1.y2/y1.y2.y3) + (y2.y3/y1.y2.y3) + (y3.y1/y1.y2.y3) = (1/y1.y2.y3)
Vereenvoudigd: (1/y3) + (1/y1) + (1/y2) = (1/y1.y2.y3) (3)
Stel a = 1/y1, b = 1/y2, c = 1/y3 en die vervangen in vergelijking (3).
Dat wordt: a + b + c = a.b.c = 1
Vermits (a.b.c=1) oneindig oplosingen heeft, heeft (a+b+c=1) dat ook.
Er zijn oneindig oplossingen..
a + b + c = a.b.c = 1 heeft oneindig oplossingen.
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
het zijn weer de laatste loodjes die zwaarst wegen,
en dan nog met een uitgedund klasje.
(-ik vraag me soms af tot hoeveel leerlingen ons klasje mag herleid
worden,vooraleer tot het 'opdoeken' van de 'school' over te gaan-).
Goed, bleven over: vragen 4 en 9.
vraag 4) Lotte - OK
er zijn inderdaad geen getallen die voldoen.
abc = 1 en a + b + c = 1. Welke pos. getallen voldoen?
Stel dat a + b + c = 1,
dan is ook (a + b + c)³ = 1
Als we (a+b+c)³ uitschrijven dan krijgen we een som van veel positieve
termen - één van deze termen is dan 6abc.
Maar abc = 1,
dus 6abc = 6 en dan is (a+b+c)³ niet meer gelijk aan 1.
Er zijn oneindig veel drietallen a, b, c waarvoor abc = 1, pastoor
voorbeeld, 2/3, 3/7 en 7/2 geven als product 1!
Er zijn ook oneindig veel drietallen a, b, c waarvoor a+b+c =1,
voorbeeld, 1/4, 1/3 en 5/12 geven als som 1!!
Maar er zijn geen a, b, c - getallen, waarvoor én abc én a+ b +c = 1!
vraag 9) pastoor - niet juist.
waarom ook niet vertrekken van een voorbeeld, en nog een, en nog een
en dan te veralgemenen.
Laat me toe te zeggen dat ik het moeilijk heb om je ganse redenering
te volgen.
Voor ieder natuurlijk getal geldt:
- OF het is een drievoud,
- OF het is een drievoud + 1,
- OF het is een drievoud + 2.
Wat weten we nu van onze vijf getallen die op een cirkel staan:
'de som van twee of drie naast elkaar liggende getallen is nooit een
drievoud'!!!
Gevraagd: ALS DAT ZO IS ... hoeveel van die getallen zijn dan zelf
een drievoud?
A) GEEN - dan hebben we vijf getallen die geen drievoud zijn.
Welnu, van iedere drie getallen die geen drievoud zijn is de som van
twee of drie van hen steeds een drievoud - kan niet - zie gegeven
B) EEN - dan hebben we vier getallen die geen drievoud zijn naast
elkaar en zie A) ... - kan niet - zie gegeven
C) DRIE - dan moeten er minstens twee drievouden naast elkaar liggen
en hebben we dus als som ook een drievoud - kan niet - zie gegeven.
D) TWEE - we leggen de twee drievouden niet naast elkaar natuurlijk en
proberen dan verder te voldoen aan ons gegeven,
zo komen we tot één van volgende schema's
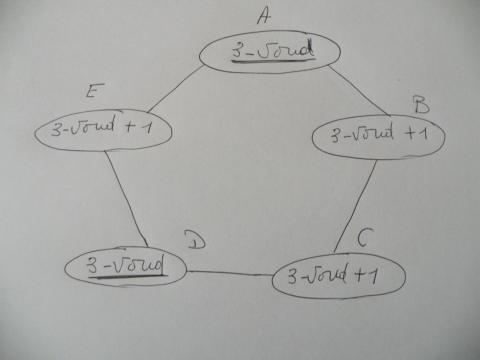
of
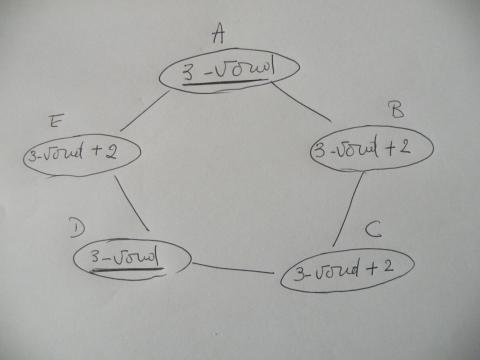
vul zelf maar gepaste getallen in ...
Besluit: als aan de gegeven voorwaarde moet voldaan worden,
hebben we steeds twee drievouden onder de vijf getallen nodig.
morgenavond een enigszins belangrijke mededeling
(- zie de aanhef van dit schrijven ...)
tot dan, denook
het zijn weer de laatste loodjes die zwaarst wegen,
en dan nog met een uitgedund klasje.
(-ik vraag me soms af tot hoeveel leerlingen ons klasje mag herleid
worden,vooraleer tot het 'opdoeken' van de 'school' over te gaan-).
Goed, bleven over: vragen 4 en 9.
vraag 4) Lotte - OK
er zijn inderdaad geen getallen die voldoen.
abc = 1 en a + b + c = 1. Welke pos. getallen voldoen?
Stel dat a + b + c = 1,
dan is ook (a + b + c)³ = 1
Als we (a+b+c)³ uitschrijven dan krijgen we een som van veel positieve
termen - één van deze termen is dan 6abc.
Maar abc = 1,
dus 6abc = 6 en dan is (a+b+c)³ niet meer gelijk aan 1.
Er zijn oneindig veel drietallen a, b, c waarvoor abc = 1, pastoor
voorbeeld, 2/3, 3/7 en 7/2 geven als product 1!
Er zijn ook oneindig veel drietallen a, b, c waarvoor a+b+c =1,
voorbeeld, 1/4, 1/3 en 5/12 geven als som 1!!
Maar er zijn geen a, b, c - getallen, waarvoor én abc én a+ b +c = 1!
vraag 9) pastoor - niet juist.
waarom ook niet vertrekken van een voorbeeld, en nog een, en nog een
en dan te veralgemenen.
Laat me toe te zeggen dat ik het moeilijk heb om je ganse redenering
te volgen.
Voor ieder natuurlijk getal geldt:
- OF het is een drievoud,
- OF het is een drievoud + 1,
- OF het is een drievoud + 2.
Wat weten we nu van onze vijf getallen die op een cirkel staan:
'de som van twee of drie naast elkaar liggende getallen is nooit een
drievoud'!!!
Gevraagd: ALS DAT ZO IS ... hoeveel van die getallen zijn dan zelf
een drievoud?
A) GEEN - dan hebben we vijf getallen die geen drievoud zijn.
Welnu, van iedere drie getallen die geen drievoud zijn is de som van
twee of drie van hen steeds een drievoud - kan niet - zie gegeven
B) EEN - dan hebben we vier getallen die geen drievoud zijn naast
elkaar en zie A) ... - kan niet - zie gegeven
C) DRIE - dan moeten er minstens twee drievouden naast elkaar liggen
en hebben we dus als som ook een drievoud - kan niet - zie gegeven.
D) TWEE - we leggen de twee drievouden niet naast elkaar natuurlijk en
proberen dan verder te voldoen aan ons gegeven,
zo komen we tot één van volgende schema's

of
vul zelf maar gepaste getallen in ...
Besluit: als aan de gegeven voorwaarde moet voldaan worden,
hebben we steeds twee drievouden onder de vijf getallen nodig.
morgenavond een enigszins belangrijke mededeling
(- zie de aanhef van dit schrijven ...)
tot dan, denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
beste leerlingen,
de klasseraad heeft een belangrijke beslissing genomen.
Voortaan gaan de veertiendaagse wiskunde-LESSEN niet meer door.
Het is nu duidelijk dat deze lessen hun vooropgesteld doel niet halen.
Er waren hier soms veel lezers, doch een continu klein aantal leerlingen.
Met de lessen trachtten we nieuwe geïnteresseerden te bereiken, die
mogelijks later ook nieuwe leerlingen zouden worden.
Op geen enkele les kregen we een reactie van een 'nieuw gezicht'.
En nu, met de droedels - toch ook iets voor niet-wiskundigen - kwam
er weer geen enkele reactie van buiten de klas.
Daarom ...
De veertiendaagse problemen en probleempjes blijven voorlopig wel
overeind. Het aantal leerlingen mag echter niet meer dalen.
Onze klas telDE vijf leerlingen.
Oomski zien we nog maar sporadisch - blijft vier leerlingen.
Troontje vertoeft aan het ander eind van de wereld - blijft drie leerlingen
Dit is het absoluut minimum.
Iedereen begrijpt dat een klas van twee leerlingen financiëel niet meer
haalbaar is. Het ministerie zal hiervoor geen erkenning meer geven. Men
kan dan beter privé-onderwijs geven ...
Besluit:
- voorlopig geen lessen meer,
- voorlopig blijven de 'problemen en probleempjes' tweewekelijks
verschijnen, behalve in de verlofperioden.
Dit zolang er minimum drie leerlingen zijn.
Volgende reeks: di 9 februari a.s.
groetjes,
denook
de klasseraad heeft een belangrijke beslissing genomen.
Voortaan gaan de veertiendaagse wiskunde-LESSEN niet meer door.
Het is nu duidelijk dat deze lessen hun vooropgesteld doel niet halen.
Er waren hier soms veel lezers, doch een continu klein aantal leerlingen.
Met de lessen trachtten we nieuwe geïnteresseerden te bereiken, die
mogelijks later ook nieuwe leerlingen zouden worden.
Op geen enkele les kregen we een reactie van een 'nieuw gezicht'.
En nu, met de droedels - toch ook iets voor niet-wiskundigen - kwam
er weer geen enkele reactie van buiten de klas.
Daarom ...
De veertiendaagse problemen en probleempjes blijven voorlopig wel
overeind. Het aantal leerlingen mag echter niet meer dalen.
Onze klas telDE vijf leerlingen.
Oomski zien we nog maar sporadisch - blijft vier leerlingen.
Troontje vertoeft aan het ander eind van de wereld - blijft drie leerlingen
Dit is het absoluut minimum.
Iedereen begrijpt dat een klas van twee leerlingen financiëel niet meer
haalbaar is. Het ministerie zal hiervoor geen erkenning meer geven. Men
kan dan beter privé-onderwijs geven ...
Besluit:
- voorlopig geen lessen meer,
- voorlopig blijven de 'problemen en probleempjes' tweewekelijks
verschijnen, behalve in de verlofperioden.
Dit zolang er minimum drie leerlingen zijn.
Volgende reeks: di 9 februari a.s.
groetjes,
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Beste Meester Denook ,
Bedankt voor uw doorzettingsvermogen bij zo weinig belangstelling !
Wij getrouwen , kijken uit naar de dinsdagavonden ......om 21:00 uur .
Ik doe een voorstel : waarom niet om 20:00 uur .
Maar er kan er maar één de eerste zijn , en hopelijk blijven er dan nog vragen over die mij ( ons ) passen ..........
Vele groetjes aan de meester en de klasgenoten
Sloeber
PS Ik doe een oproep om mee te doen , vooral naar Troontje en Oomski ! Wij missen U ! Sluit terug aan bij ons vrolijk klasje .........
Bedankt voor uw doorzettingsvermogen bij zo weinig belangstelling !
Wij getrouwen , kijken uit naar de dinsdagavonden ......om 21:00 uur .
Ik doe een voorstel : waarom niet om 20:00 uur .
Maar er kan er maar één de eerste zijn , en hopelijk blijven er dan nog vragen over die mij ( ons ) passen ..........
Vele groetjes aan de meester en de klasgenoten
Sloeber
PS Ik doe een oproep om mee te doen , vooral naar Troontje en Oomski ! Wij missen U ! Sluit terug aan bij ons vrolijk klasje .........
Meten is weten - Carpe diem
-
oomski - Lid geworden op: 28 mei 2008, 08:25
- Locatie: Thuis.
Hey, ik ben er nog wel en kom altijd kijken. Maar het is zoals meester denook zegt, de lessen hebben niet hun bedoelde resultaat, ook niet bij mij.  En waarom? Ik kan het niet meer opbrengen om me de nieuwe dingen in te prenten, spijtig genoeg.
En waarom? Ik kan het niet meer opbrengen om me de nieuwe dingen in te prenten, spijtig genoeg.
Maar ik zie wel wat ik kan proberen en dan doe ik het wel.
En idd. een dikke pluim voor de meester om zijn doorzetting.
Maar ik zie wel wat ik kan proberen en dan doe ik het wel.
En idd. een dikke pluim voor de meester om zijn doorzetting.
Wie op wraak zint, houdt zijn eigen wonden open.
-
lotte - Lid geworden op: 26 apr 2005, 13:47
- Locatie: Tielt
hallo iedereen,
zal me ook maar eens laten horen zeker,
zo komt onze topic weer wat omhoog.
Beste sloeberkebebo, voor mij is 20 uur ook goed,
maar moet de meester daar niet over beslissen?
Hij zal zelf nog wel reageren denk ik,
nu hij leest hoe graag we hem allemaal lezen.
Misschien neemt hij 21 uur omdat er velen
zijn die naar 'thuis' kijken; enfin ik weet het niet.
Wat vindt pastoor van het uur, en troontje
(-als ze al terug is-), en oomski en ...
oei, er zijn er geen meer.
goede avond iedereen,
lotte
zal me ook maar eens laten horen zeker,
zo komt onze topic weer wat omhoog.
Beste sloeberkebebo, voor mij is 20 uur ook goed,
maar moet de meester daar niet over beslissen?
Hij zal zelf nog wel reageren denk ik,
nu hij leest hoe graag we hem allemaal lezen.
Misschien neemt hij 21 uur omdat er velen
zijn die naar 'thuis' kijken; enfin ik weet het niet.
Wat vindt pastoor van het uur, en troontje
(-als ze al terug is-), en oomski en ...
oei, er zijn er geen meer.
goede avond iedereen,
lotte
Laatst gewijzigd door lotte op 05 feb 2010, 16:56, 2 keer totaal gewijzigd.
-
oomski - Lid geworden op: 28 mei 2008, 08:25
- Locatie: Thuis.
Hallo iedereen
Voor mij is het om het even welk uur hoor. Ik besef vaak niet dat het al 21u is en dan ben ik toch zowiezo niet de eerste, maar dat hoeft ook niet.
Laat maar horen(lezen)
Sweet dreams allemaal.
Voor mij is het om het even welk uur hoor. Ik besef vaak niet dat het al 21u is en dan ben ik toch zowiezo niet de eerste, maar dat hoeft ook niet.
Laat maar horen(lezen)
Sweet dreams allemaal.
Wie op wraak zint, houdt zijn eigen wonden open.
-
troontje - Lid geworden op: 14 dec 2004, 10:03
Goede morgen,
-Meester ik ben vanaf nu weer trouw in de klas aanwezig ( de "10 probleempjes),wil je dit overmaken aan de klasseraad,zodat het ministerie van onderwijs erkenning blijft geven voor de kleine maar toffe klas!
-Hartelijke dank meester dat je onze meester wil zijn!
-Hartelijke dank ook aan de slimme klasgenoten om niet metteen de gemakkelijkste oefening op te lossen!
-Bedankt Lotte voor de vakantiewensen,wij hebben ervan genoten!
groetjes,
troontje
-Meester ik ben vanaf nu weer trouw in de klas aanwezig ( de "10 probleempjes),wil je dit overmaken aan de klasseraad,zodat het ministerie van onderwijs erkenning blijft geven voor de kleine maar toffe klas!
-Hartelijke dank meester dat je onze meester wil zijn!
-Hartelijke dank ook aan de slimme klasgenoten om niet metteen de gemakkelijkste oefening op te lossen!
-Bedankt Lotte voor de vakantiewensen,wij hebben ervan genoten!
groetjes,
troontje
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
Hallo, hallo,
zowat iedereen is aan het woord geweest, waarvoor dank.
Dus morgen zijn we er weer met de 'problemen en probleempjes'.
Alleen, hoe laat?
Sloeberkebebo heeft liever 20 uur -
oomski en lotte hebben daar geen probleem mee -
pastoor en troontje reageren niet, dus ook ok? ...
Voor mij om het even; ik bak de broodjes vandaag
en zet ze morgen om 20 uur in de oven,
tenzij er toch nog tegenwind komt voor 20 uur.
Ik ken mijn leerlingen stilaan wel hoor:
- sloeberkebebo heeft graag iets met tekeningen,
- oomski valt op vraagstukken die leiden tot vergelijkingen,
- troontje probeert en probeert tot ze het vindt - vraag haar niet hoe ...
- pastoor spint alles graag uit, liefst met een bewijs,
- lotte, ja, daar weet ik minst van, alhoewel ze meer dan haar plan trekt
en er gewoonlijk als eerste bij is.
Bij iedere reeks oefeningen tracht ik er voor elk wat wils in te steken,
wat ook dikwijls lukt, gezien de weinige fouten de laatste tijd.
tot morgen dan, 20 uur,
groetjes, denook
zowat iedereen is aan het woord geweest, waarvoor dank.
Dus morgen zijn we er weer met de 'problemen en probleempjes'.
Alleen, hoe laat?
Sloeberkebebo heeft liever 20 uur -
oomski en lotte hebben daar geen probleem mee -
pastoor en troontje reageren niet, dus ook ok? ...
Voor mij om het even; ik bak de broodjes vandaag
en zet ze morgen om 20 uur in de oven,
tenzij er toch nog tegenwind komt voor 20 uur.
Ik ken mijn leerlingen stilaan wel hoor:
- sloeberkebebo heeft graag iets met tekeningen,
- oomski valt op vraagstukken die leiden tot vergelijkingen,
- troontje probeert en probeert tot ze het vindt - vraag haar niet hoe ...
- pastoor spint alles graag uit, liefst met een bewijs,
- lotte, ja, daar weet ik minst van, alhoewel ze meer dan haar plan trekt
en er gewoonlijk als eerste bij is.
Bij iedere reeks oefeningen tracht ik er voor elk wat wils in te steken,
wat ook dikwijls lukt, gezien de weinige fouten de laatste tijd.
tot morgen dan, 20 uur,
groetjes, denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
Dinsdagavond 20 uur: 'wiskundige problemen en probleempjes',
op een nieuw, vroeger uur

3) Een auto legt in 3 uur 255 km af. Het eerste deel rijdt hij tegen 100 km/uur. Het tweede
deel tegen 80 km per uur. Hoe lang reed hij tegen 100 km/uur?
4) Het middelpunt van het bovenvlak van een kubus met ribbe 2, ligt op gelijke afstand
van de vier hoekpunten van het grondvlak. Hoe groot is die afstand?
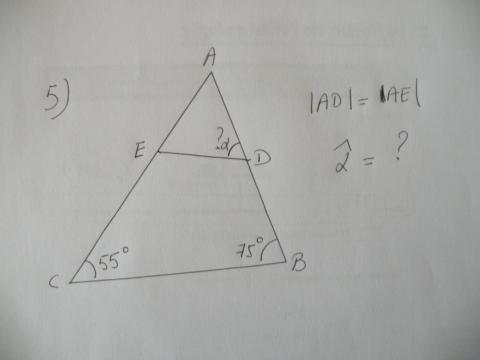
6) Plaatsen we achter een getal twee nullen, dan vinden we een getal dat 297 meer is
dan het oorspronkelijke getal. Wat was dat oorspronkelijke getal?
7) Ik schrijf alle mogelijke getallen van zes cijfers, door alleen 1 en 2 te gebruiken,
(-voorbeeld: 211222-). Als ik uit die rij getallen een willekeurig getal aanduid, wat is
dan de kans dat er precies driemaal een '1' in staat, en wel de drie 'enen'
naast elkaar?
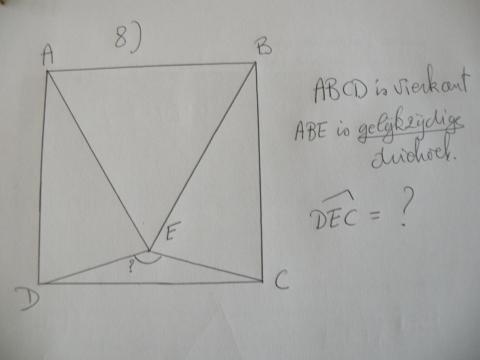
9) Nonkel Frans is over 15 jaar, vijf keer zo oud als 25 jaar geleden. Hoe oud is hij nu?
10) Als A, B en C cijfers zijn , en AAA + B = BCCC, wat zijn dan A, B en C?
ziezo, dat waren ze weer -
nieuwe leerlingen graag welkom (- ze lezen wel eerst blz 1-)
tot morgen,
denook
een extraatje:
schrijf een willekeurig getal van drie cijfers,
schrijf er nog eens hetzelfde getal naast;
nu heb je een getal van zes cijfers geschreven, deelbaar door 7, door 11 en door 13.
op een nieuw, vroeger uur

3) Een auto legt in 3 uur 255 km af. Het eerste deel rijdt hij tegen 100 km/uur. Het tweede
deel tegen 80 km per uur. Hoe lang reed hij tegen 100 km/uur?
4) Het middelpunt van het bovenvlak van een kubus met ribbe 2, ligt op gelijke afstand
van de vier hoekpunten van het grondvlak. Hoe groot is die afstand?
6) Plaatsen we achter een getal twee nullen, dan vinden we een getal dat 297 meer is
dan het oorspronkelijke getal. Wat was dat oorspronkelijke getal?
7) Ik schrijf alle mogelijke getallen van zes cijfers, door alleen 1 en 2 te gebruiken,
(-voorbeeld: 211222-). Als ik uit die rij getallen een willekeurig getal aanduid, wat is
dan de kans dat er precies driemaal een '1' in staat, en wel de drie 'enen'
naast elkaar?

9) Nonkel Frans is over 15 jaar, vijf keer zo oud als 25 jaar geleden. Hoe oud is hij nu?
10) Als A, B en C cijfers zijn , en AAA + B = BCCC, wat zijn dan A, B en C?
ziezo, dat waren ze weer -
nieuwe leerlingen graag welkom (- ze lezen wel eerst blz 1-)
tot morgen,
denook
een extraatje:
schrijf een willekeurig getal van drie cijfers,
schrijf er nog eens hetzelfde getal naast;
nu heb je een getal van zes cijfers geschreven, deelbaar door 7, door 11 en door 13.
Laatst gewijzigd door denook op 09 feb 2010, 20:05, 1 keer totaal gewijzigd.