Wiskundige problemen en probleempjes 2

[denook]

nog een late goeie avond iedereen,

we wachten niet meer tot morgen,
de laatste twee problemen zijn immers opgelost,
proficiat lotte en pastoor,
en iedereen van onze klas die weer meespeelde,
met een speciale vermelding voor de mooie
figuren van de hand van sloeberkebebo.

tot dinsdag 1 juni,
slaap wel,
denook

[denook]

Dinsdag 1 juni 2010 - tien wiskundige problemen en probleempjes,





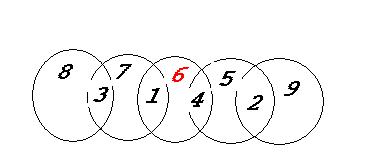
In ieder deel van elke cirkel komt een cijfer van 1 tot 9, alle verschillend.
De som der cijfers in iedere cirkel is 11.
Welk cijfer staat op de plaats van het vraagteken?

2) We weten dat 5.a.m. hetzelfde betekent als 5 uur 's morgens (-vóór de middag-)en 5.p.m. hetzelfde als 5 uur 's avonds (- na de middag-) of 17 uur.
Als het nu 8.a.m. is, hoe laat is het dan binnen 2010 uren?

3) Grootmoeder bakt een cake voor haar kleinkinderen die straks komen. Ze wil de cake zo verdelen dat ieder kind evenveel krijgt. Ze is echter vergeten of ze nu 3 of 5 of 6 kleinkinderen heeft. In hoeveel stukken moet ze nu de cake snijden om op alles voorbereid te zijn?

4) Welke kans is de grootste?
a) een muntstuk tienmaal opgooien met telkens de muntzijde naar boven,
b) een dobbelsteen viermaal gooien met telkens de '1' naar boven.

5) Wat is het gemiddelde van 1/0,22222...en 1/0,66666...?

6) Luca heeft 18 minuten nodig om drie korte kettingen te verbinden tot één lange ketting.
Hoeveel tijd heeft hij nodig om zes korte kettingen te verbinden tot één lange ketting?





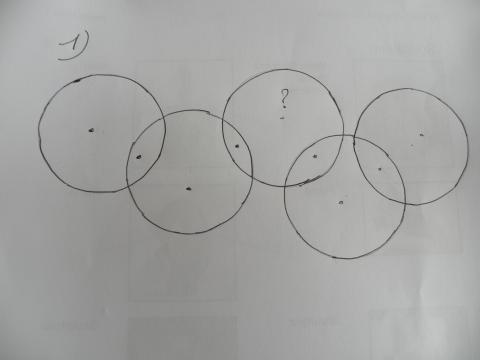
Als je weet dat de oppervlakte van het vierde deel van de kleine cirkel gelijk is aan de oppervlakte van de ring tussen beide cirkels, wat is dan de verhouding van de omtrek van de kleine cirkel tot de omtrek van de grote cirkel?

8 ) We beschouwen volgende functie f,
f(n) = n/2 als n even is, voorbeeld f(36) = 18, en
f(n) = 4.n 1 als n oneven is, voorbeeld f(7) = 29
Zo is dus f(f(22)) = f(11) = 45
Voor welke n-waarde(n) is f(f(n)) = 21?




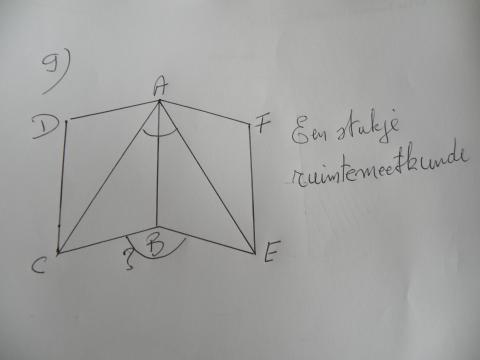
ABCD en ABEF zijn twee vierkanten in de ruimte met gemeenschappelijke zijde AB. Als de hoek tussen de diagonalen CA en EA gelijk is aan 60°, hoe groot (+ waarom?) is dan de hoek CBE?

10) In een hoek van een zuiver rechthoekige kamer staat een ronde tafel tegen de muren gedrukt. De afstand van de tafel tot het hoekpunt is 230 mm.
Bereken de diameter van de tafel.

Veel succes iedereen en denk er aan: één oefening per leerling per 24 uur.
Tot morgen,
denook

[pastoor]

vraag 4

Muntstuk: (1/2) tot de macht 10 = 1/1024.
Dobbelsteen: (1/6) tot de macht 4 = 1/1296.

antwoord a.

[lotte]

Goeie avond denook,

vraag 3
kgv 3.5.6. = 30

Oma verdeelt de taart voor best in 30 stukken

groetjes allen
lotte.

[sloeberkebebo]

Goede avond allemaal

Vraag 9

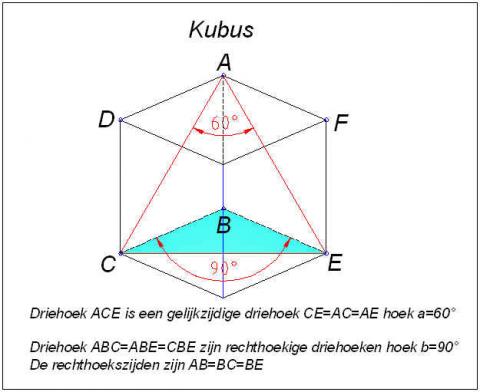
Driehoek ACE is een gelijkzijdige driehoek CE=AC=AE hoek a=60°

Driehoek ABC=ABE=CBE zijn rechthoekige driehoeken hoek b=90°
De rechthoekszijden zijn AB=BC=BE


Groetjes

Sloeber

[troontje]

goede avond iedereen,

vraag1,




troontje,

[oomski]

Goede avond allen.
Vraag 6:

2 verbindingen in 18'
5 verbindingen in (18x5)/2 = 45'

[denook]

minder dan 24 uur later,
265 binnenkijkers later ...

de vijf leerlingen (-wanneer een zesde?-) beantwoordden ieder
een vraag; en hoe?

vraag 4) pastoor - ok - en vliegensvlug,

vraag 3) lotte - ok - grootmoe zal blij zijn voor de hulp,

vraag 9) sloeberkebebo - ok - maar toch ...
waarom is driehoek CBE precies rechthoekig ...
als de zijden van de vierkanten gelijk zijn aan 1,
dan zijn AC en AE gelijk aan wortel2 (-Pythagoras-) -
CAE is inderdaad gelijkzijdig, want gelijkbenig met tophoek van 60° -
dus is CE ook gelijk aan wortel2, en omdat CB = BE = 1 zal de hoek
CBE gelijk moeten zijn aan 90° (-omgekeerde van Pythagoras-).
Heb jij een andere juiste redenering sloeberkebebo, om aan te tonen
dat de hoek 90° is, geef maar door.

vraag 1) - troontje - ok - knap werk
we voelen aan dat de buitenste stukken 8 en 9 moeten bevatten;
daarna is het prutswerk. Men zou geneigd zijn om bij het vraagteken een
5 te plaatsen (-ligt midden in de rij van 1 tot 9-), doch zo komt men er
niet; het is inderdaad een 6 die we nodig hebben.

vraag 6) - oomski - ok,
een klein bijvraagje, alleen voor oomski!!
We kunnen een hond aan de 'KETTING' leggen
(-we hebben dan een LANGE ketting van A tot B-)
Zo loste jij het vraagje correct op.
We kunnen ook een halsKETTING of een tandwielKETTING hebben
(-we hebben dan een GESLOTEN ketting).
Beste oomski, als de drie kleine kettingen gesloten waren en ze moeten
open gemaakt worden en dan tot één nieuwe gesloten ketting verbonden,
en als gans dat proces 18 minuten duurt ... hoelang duurt het dan om
van onze zes kleine gesloten kettingen één grote gesloten ketting te
maken?

we zijn al half-weg,
tot morgen, denook

[pastoor]

Goede avond Denook en de medeleerlingen.

Vraag 10) In een hoek van een zuiver rechthoekige kamer staat een ronde tafel tegen de muren gedrukt. De afstand van de tafel tot het hoekpunt is 230 mm. Bereken de diameter van de tafel.

Stel r is de straal van de tafel, en 230 mm = 23 cm.
Dan is (pythagoras) r² + r² = (r + 23)² = r² + (2 * 23 * r) + (23)².
Of r² = (46 * r) + (23)²
Of r² - 46r - 529 = 0. Een vierkantsvergelijking.

Vierkantsvergelijking oplossen.
* Discriminant D = (-46)² - 4*(-529) = 2116 + 2116 = 4232.
* √D = √4232
* 46 + √D, +46 - √D
* Mogelijke oplossingen : X1 = (+46 - √D)/2, en X2 = (+46 + √D)/2

Oplossingen.
X2 = (+46 - √D)/2 = (46 - √4232)/2 = kleiner dan 0 en geen oplossing.

X1 = (+46 + √D)/2.
Diameter is tweemaal de straal of tweemaal X1 (in cm).
Diameter is = (+46 + √D) = (46 + √(4232)) = 46 + 65,054 = 111,054 cm

Antwoord: 111,054 cm

[lotte]

Iederéén een goeie avond

2) We weten dat 5.a.m. hetzelfde betekent als 5 uur 's morgens (-vóór de middag-)en 5.p.m. hetzelfde als 5 uur 's avonds (- na de middag-) of 17 uur.
Als het nu 8.a.m. is, hoe laat is het dan binnen 2010 uren?

2010 uren = 83.75 dagen
0.75 dag = 18 uur
8.a.m. + 18 uur = 26 uur
antw. 2.a.m.

[sloeberkebebo]

goede avond allemaal

Vraag 10

Anders berekend , zelfde resultaat . De maten zijn in mm .
Diameter is 1110,54



Groetjes

Sloeber

[sloeberkebebo]

Goede avond allemaal

Vraag 7



Groetjes

Sloeber

[oomski]

vraag 6) - oomski - ok,
een klein bijvraagje, alleen voor oomski!!
We kunnen een hond aan de 'KETTING' leggen
(-we hebben dan een LANGE ketting van A tot B-)
Zo loste jij het vraagje correct op.
We kunnen ook een halsKETTING of een tandwielKETTING hebben
(-we hebben dan een GESLOTEN ketting).
Beste oomski, als de drie kleine kettingen gesloten waren en ze moeten
open gemaakt worden en dan tot één nieuwe gesloten ketting verbonden,
en als gans dat proces 18 minuten duurt ... hoelang duurt het dan om
van onze zes kleine gesloten kettingen één grote gesloten ketting te
maken?

Ja meester denook, ik dacht aan een losse ketting.

Als ze dicht moeten dan is de oplossing natuurlijk:
3verbindingen in 18'
Dus 6 verbindingen in (18x6)/3 = 36'

[troontje]

goede avond iedereen,


ik had geprobeerd om vraag 7 op te lossen,op een andere manier dan jou sloeberkebebo, waar ik natuurlijk niet aan twijfel dat jouw oplossing zeker juist is,'k zou niet durven

mijn oplossing is,


-straal 5 cm(kleine cirkel)
oppervlakte kleine cirkel=3,14x5x5=78,50 : 4=19,62(oppervlakte 1/4 van kleine cirkel)
oppervlakte grote cirkel=78,50+19,62=98,12


omtrek kleine cirkel=3,14x10=31,40 :4=7,85
omtrek grote cirkel=31,40+7,85=38,25

verhouding =4/5


troontje

[pastoor]

Vraag 7 berekend

Stel r de straal van de kleine cirkel en R de straal van de grote cirkel.
Oppervlakte kleine cirkel = π * r² en oppervlakte grote cirkel is π * R².
Dan is (5/4) * π * r² = π * R², en vereenvoudigd r = R * √(4/5).
De omtrek (2 * π * r) = (2* π * R) * √(4/5).
Antwoord (omtrek kleine cirkel/omtrek grote cirkel) = √(4/5).