Wiskundige problemen en probleempjes 2
-
oomski - Lid geworden op: 28 mei 2008, 08:25
- Locatie: Thuis.
1/0,22222 = 4,500045lotte schreef:Geef je mijn getallen oomski, zou niet de eerste keer zijn dat mijn rekenmachientje fout...
1/0.2222 = 4.5004500
1/0.6666 = 1.5001500
1/0,66666 = 1,500015
(4,500045 + 1,500015)/2 = 3,00003
Het verschil zit hem in het aantal 2's en 6'en die gebruikt worden denk ik.
Zijn er maar 3 2's en 3 6'en dan is er na de 5 maar één nul.
Laatst gewijzigd door oomski op 03 jun 2010, 13:02, 1 keer totaal gewijzigd.
Wie op wraak zint, houdt zijn eigen wonden open.
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
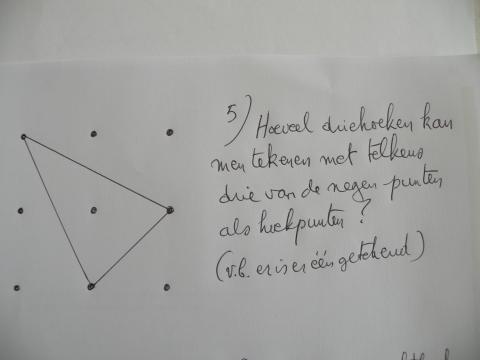
vraag 5.
de opgave is 1/0,2222....... oneindig aantal cijfers 2 en idem voor 6.
vraag 5) Wat is het gemiddelde van 1/0,22222...en 1/0,66666...?
Als men in 1/0,2222... teller en noemer vermenigvuldigt met 3, dan kan men de twee termen optellen; en 0,666666... is 2/3.
(1/0,22222... + 1/0,66666… )/2 = [3/(2/3) + 1/(2/3)]/2
= (4/(2/3))/2 = 3
Antwoord: 3
de opgave is 1/0,2222....... oneindig aantal cijfers 2 en idem voor 6.
vraag 5) Wat is het gemiddelde van 1/0,22222...en 1/0,66666...?
Als men in 1/0,2222... teller en noemer vermenigvuldigt met 3, dan kan men de twee termen optellen; en 0,666666... is 2/3.
(1/0,22222... + 1/0,66666… )/2 = [3/(2/3) + 1/(2/3)]/2
= (4/(2/3))/2 = 3
Antwoord: 3
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
minder dan 48 uur later,
459 binnenkijkers later,
wat een gezellige drukte hier,
we gaan verder
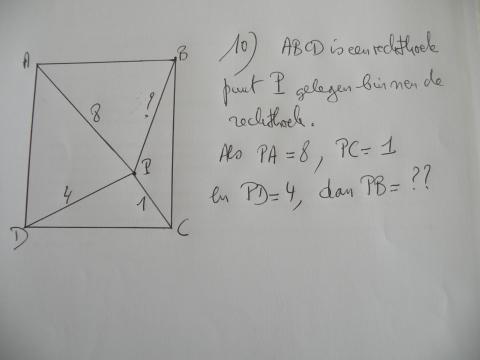
vraag 10) pastoor en sloeberkebebo - beiden ok
vraag 2) lotte - ok
vraag 7) pogingen van sloeberkebebo, troontje en pastoor,
overal juiste delen in berekeningen, met pastoor exact resultaat
nog eens (-klaar?-) uitgelegd:
r staal kleine cirkel, dan oppervlakte: pi.r²
R straal grote cirkel, dan oppervlakte: pi.R²
oppervlakte ring: pi.R² - pi.r² (1)
nu is (1) ook gelijk aan de oppervlakte van vierde deel kleine cirkel,
dat geeft: pi.R² - pi.r² = pi.r²/4
pi.R² = pi.r² + pi.r²/4
pi.R² = (5/4).pi.r²
R² = (5/4).r²
R = wortel(5/4) . r
omtrek kleine cirkel: 2.pi.r (2)
omtrek grote cirkel: 2.pi.R = 2.pi.wortel(5/4).r (3)
gevraagde verhouding, of (2)/(3)
2.pi.r / 2.pi.wortel(5/4).r = 1 / wortel(5/4) = wortel(4/5) = 2/wortel5
= 0,89442791... (- zie pastoor en zie bijna sloeberkebebo)
vraag 6 bis) - oomski ok
vraag 5) oomski ok - in iets mindere mate lotte - correct pastoor
nog een andere benadering
0,2222222... = 2/9 (-zie lessen van weleer-),
0,6666666... = 6/9 (- idem -)
daarom: 1/0,22222... = 9/2
en 1/0,666666... = 9/6 = 3/2
en dan gemiddelde van de twee waarden:
(9/2 + 3/2)/2 = (12/2)/2 = 6/2 = 3
blijft over: vraag 8 -
traag lezen, geen schrik van de f(...), niet moeilijk
tot morgen?
denook
459 binnenkijkers later,
wat een gezellige drukte hier,
we gaan verder
vraag 10) pastoor en sloeberkebebo - beiden ok
vraag 2) lotte - ok
vraag 7) pogingen van sloeberkebebo, troontje en pastoor,
overal juiste delen in berekeningen, met pastoor exact resultaat
nog eens (-klaar?-) uitgelegd:
r staal kleine cirkel, dan oppervlakte: pi.r²
R straal grote cirkel, dan oppervlakte: pi.R²
oppervlakte ring: pi.R² - pi.r² (1)
nu is (1) ook gelijk aan de oppervlakte van vierde deel kleine cirkel,
dat geeft: pi.R² - pi.r² = pi.r²/4
pi.R² = pi.r² + pi.r²/4
pi.R² = (5/4).pi.r²
R² = (5/4).r²
R = wortel(5/4) . r
omtrek kleine cirkel: 2.pi.r (2)
omtrek grote cirkel: 2.pi.R = 2.pi.wortel(5/4).r (3)
gevraagde verhouding, of (2)/(3)
2.pi.r / 2.pi.wortel(5/4).r = 1 / wortel(5/4) = wortel(4/5) = 2/wortel5
= 0,89442791... (- zie pastoor en zie bijna sloeberkebebo)
vraag 6 bis) - oomski ok
vraag 5) oomski ok - in iets mindere mate lotte - correct pastoor
nog een andere benadering
0,2222222... = 2/9 (-zie lessen van weleer-),
0,6666666... = 6/9 (- idem -)
daarom: 1/0,22222... = 9/2
en 1/0,666666... = 9/6 = 3/2
en dan gemiddelde van de twee waarden:
(9/2 + 3/2)/2 = (12/2)/2 = 6/2 = 3
blijft over: vraag 8 -
traag lezen, geen schrik van de f(...), niet moeilijk
tot morgen?
denook
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Goede avond Denook en alle anderen.
Vraag 8 ) We beschouwen volgende functie f, f(n) = n/2 als n even is, voorbeeld f(36) = 18, en f(n) = 4.n 1 als n oneven is, voorbeeld f(7) = 29
Zo is dus f(f(22)) = f(11) = 45. Voor welke n - waarde(n) is f(f(n)) = 21?
* * * * *
f(f(10)) = f(5) want (n = 10) of even en dus n/2 of 10/2 = 5.
f(5) = 21, want (n=5) of oneven en dus 4n + 1 of (4*5) + 1 = 21.
Antwoord f(f(10)) = f(5) = 21.
Als n in f(f(n) een oneven getal is, dan wordt 1, 3, 5, 7, enz. … 3, 7, 11, 15 enz. Als n in f(f(n) een even getal is, dan wordt 2, 4, 6, 8, enz. … 5, 9, 13, 17 enz. Dan is er maar een oplossing met resultaat 21.
* * * * *
Maar met meer functies:
Ook f(f(f(2))) = f(f(1)) = f(5) = 21.
Ook f(f(f(f(4)))) = f(f(f(2))) = f(f(1)) = f(5) = 21.
Ook f(f(f(f(f(8))))) = f(f(f(f(4)))) = f(f(f(2))) = f(f(1)) = f(5) = 21.
En zo voort.
Ook f(f(f(20))) = f(f(10)) = f(5) = 21.
Ook f(f(f(f(40)))) = f(f(f(20))) = f(f(10)) = f(5) = 21.
Ook f(f(f(f(f(80))))) = f(f(f(f(40)))) = f(f(f(20))) = f(f(10)) = f(5) = 21.
En zo voort.
Vraag 8 ) We beschouwen volgende functie f, f(n) = n/2 als n even is, voorbeeld f(36) = 18, en f(n) = 4.n 1 als n oneven is, voorbeeld f(7) = 29
Zo is dus f(f(22)) = f(11) = 45. Voor welke n - waarde(n) is f(f(n)) = 21?
* * * * *
f(f(10)) = f(5) want (n = 10) of even en dus n/2 of 10/2 = 5.
f(5) = 21, want (n=5) of oneven en dus 4n + 1 of (4*5) + 1 = 21.
Antwoord f(f(10)) = f(5) = 21.
Als n in f(f(n) een oneven getal is, dan wordt 1, 3, 5, 7, enz. … 3, 7, 11, 15 enz. Als n in f(f(n) een even getal is, dan wordt 2, 4, 6, 8, enz. … 5, 9, 13, 17 enz. Dan is er maar een oplossing met resultaat 21.
* * * * *
Maar met meer functies:
Ook f(f(f(2))) = f(f(1)) = f(5) = 21.
Ook f(f(f(f(4)))) = f(f(f(2))) = f(f(1)) = f(5) = 21.
Ook f(f(f(f(f(8))))) = f(f(f(f(4)))) = f(f(f(2))) = f(f(1)) = f(5) = 21.
En zo voort.
Ook f(f(f(20))) = f(f(10)) = f(5) = 21.
Ook f(f(f(f(40)))) = f(f(f(20))) = f(f(10)) = f(5) = 21.
Ook f(f(f(f(f(80))))) = f(f(f(f(40)))) = f(f(f(20))) = f(f(10)) = f(5) = 21.
En zo voort.
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
toch even tussen komen ...
beste pastoor en anderen,
als f(f(n)) = 21,
dan kan f(n) = 5 en dan f(5) = 21 en dus n = 10
op een rijtje ...
f(f(10)) = f(5) = 21
maar er zijn nog oplossingen voor n ....
wie zoekt verder?
en nu tot morgen,
denook
beste pastoor en anderen,
als f(f(n)) = 21,
dan kan f(n) = 5 en dan f(5) = 21 en dus n = 10
op een rijtje ...
f(f(10)) = f(5) = 21
maar er zijn nog oplossingen voor n ....
wie zoekt verder?
en nu tot morgen,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
sorry mensen,
sloeberkebebo roept me nog even terug
bij vraag 7) was het exacte antwoord: 2 / wortel5
ik berekende dit met een zakrekenmachine
en vond 0,894427191...,
ik typte echter 0,89442791,
of ik vergat de '1' op de zevende plaats na de komma
sloeberkebebo merkte dit foutje op
en liet het me discreet privé weten,
waarvoor dank.
En zo is het nu helemaal correct 'getypt',
denook
sloeberkebebo roept me nog even terug
bij vraag 7) was het exacte antwoord: 2 / wortel5
ik berekende dit met een zakrekenmachine
en vond 0,894427191...,
ik typte echter 0,89442791,
of ik vergat de '1' op de zevende plaats na de komma
sloeberkebebo merkte dit foutje op
en liet het me discreet privé weten,
waarvoor dank.
En zo is het nu helemaal correct 'getypt',
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
we sluiten weer onze reeks problemen en probleempjes af.
Inderdaad pastoor, voor vraag 8 waren er nog twee andere
antwoorden, in totaal dus drie: n = 10, n = 1 en n = 84; mooi gevonden.
Je andere mogelijk antwoord, n = 10,25, kan niet aanvaard worden.
Als we in de opgave spreken van 'even' en 'oneven' getallen voor n,
dan moeten dat gehele getallen zijn.
Is 10,25 oneven? en 10,250 even?
We onthouden voor later misschien dat bij opgaven met 'even' en 'oneven'
steeds met gehele getallen wordt gewerkt.
Het was weer een boeiende bedoening, met de ganse klas heel actief.
Mooi zo.
Volgende problemenreeks op dinsdag 15 juni a.s.
Dit zal dan misschien de laatste, of hoogstens de voorlaatste zijn ...
vòòr het grote verlof.
tot dan,
denook
we sluiten weer onze reeks problemen en probleempjes af.
Inderdaad pastoor, voor vraag 8 waren er nog twee andere
antwoorden, in totaal dus drie: n = 10, n = 1 en n = 84; mooi gevonden.
Je andere mogelijk antwoord, n = 10,25, kan niet aanvaard worden.
Als we in de opgave spreken van 'even' en 'oneven' getallen voor n,
dan moeten dat gehele getallen zijn.
Is 10,25 oneven? en 10,250 even?
We onthouden voor later misschien dat bij opgaven met 'even' en 'oneven'
steeds met gehele getallen wordt gewerkt.
Het was weer een boeiende bedoening, met de ganse klas heel actief.
Mooi zo.
Volgende problemenreeks op dinsdag 15 juni a.s.
Dit zal dan misschien de laatste, of hoogstens de voorlaatste zijn ...
vòòr het grote verlof.
tot dan,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond aan alle spelers
en supporters langs de zijlijn,
we naderen het einde van het schooljaar.
Dinsdag 15 juni is de laatste 'proef'.
Er is ook nog dinsdag 29 juni, maar ...
- in welke school zijn er nog proeven op 29 juni,
- wanneer moet er dan gedelibereerd worden?
We willen op 29 juni de lijst bekend maken
van de geslaagden voor dit schooljaar.
Omdat dinsdag 15 juni dus de laatste
'wiskundige problemen en probleempjes'-dag is,
en we in schoonheid willen eindigen,
voorzien we voor die dag geen 10, maar wel 15 vraagjes.
tot dan,
denook
en supporters langs de zijlijn,
we naderen het einde van het schooljaar.
Dinsdag 15 juni is de laatste 'proef'.
Er is ook nog dinsdag 29 juni, maar ...
- in welke school zijn er nog proeven op 29 juni,
- wanneer moet er dan gedelibereerd worden?
We willen op 29 juni de lijst bekend maken
van de geslaagden voor dit schooljaar.
Omdat dinsdag 15 juni dus de laatste
'wiskundige problemen en probleempjes'-dag is,
en we in schoonheid willen eindigen,
voorzien we voor die dag geen 10, maar wel 15 vraagjes.
tot dan,
denook
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
dinsdag 15 juni 2010,
Hallo iedereen,
laatste problemen en probleempjes van dit schooljaar?
1)Een computer zendt boodschappen uit, telkens bestaande uit drie cijfers, en wel alleen gebruik makend van 0 en 1.
Welke van volgende uitspraken zijn waar?
A) als het eerste cijfer een 0 is, is de som der cijfers kleiner dan 3,
B) als de som der cijfers oneven is, is het eerste of derde cijfer een 1,
C) de som der cijfers is oneven als en slechts als er minstens één 1 bij is,
D) er is minstens één 1 als de som der cijfers oneven is.
2) Als bij de reële getallen, verschillend van 0 geldt dat a < b en c < d, welke van volgende beweringen zijn dan ook juist?
A) a - c < b - d, B) a - d < b - c, C) a.c < b.c, D) 1 / b < 1 / a.
3) Welke van volgende lijnen verdeelt een driehoek in twee even grote delen?
A) een hoogtelijn, B) een bissectrice van een hoek, C) een zwaartelijn,
E) een middelloodlijn van een zijde.
4) Ik beschouw de getallen 4, 8, 9, 16, 27, 32, 64, 81 en 243. Als ik telkens twee van deze getallen vermenigvuldig, hoeveel verschillende resultaten kan ik dan bekomen?
6)De helft van 8a / 12 is? A) 2a / 3, B) a / 3, C) 4a / 3, D) 4a / 24,
E) 4a / 6.
7) Een moderne voetbal is opgebouwd uit 12 vijfhoeken en 20 zeshoeken. Hoeveel ribben telt de bal?
8 ) Hoe kun je tien bomen planten zodat je vijf rijen van vier bomen ziet?
9) Kamelixen hebben 3 keer meer bulten dan dromedixen. Een gemengde kudde van 24 dieren heeft samen evenveel bulten als 10 dromedixen en 6 kamelixen samen. Hoeveel dromedixen zijn er in de kudde?
11) De moeder van David en Sofie is in verwachting van een baby. Als het een meisje wordt heeft David tweemaal zoveel zussen als broers; als het een jongen wordt heeft Sofie tweemaal zoveel broers als zussen. Hoeveel kinderen heeft moeder ... de toekomstige baby niet meegerekend?
12 ...een moeilijke ... tracht 21 te bekomen door 1, 5, 6 en 7 ieder éénmaal te gebruiken en verder alleen met de bewerkingen optellen, aftrekken, vermenigvuldigen en delen.te werken. Let op: de bewerkingen moeten niet noodzakelijk allemaal voorkomen. Prutswerk ...

15) De diagonalen van een ruit hebben als lengten 3 en 7,20 meter. De afstand tussen de evenwijdige zijden is dan gelijk aan ?
A) 12 / 5, B) 36 /13, C) 18 / 13, D) 72 / 13, E) 36 / 17
tot daar een langere afsluiter,
rustig aan en veel succes,
denook
Hallo iedereen,
laatste problemen en probleempjes van dit schooljaar?
1)Een computer zendt boodschappen uit, telkens bestaande uit drie cijfers, en wel alleen gebruik makend van 0 en 1.
Welke van volgende uitspraken zijn waar?
A) als het eerste cijfer een 0 is, is de som der cijfers kleiner dan 3,
B) als de som der cijfers oneven is, is het eerste of derde cijfer een 1,
C) de som der cijfers is oneven als en slechts als er minstens één 1 bij is,
D) er is minstens één 1 als de som der cijfers oneven is.
2) Als bij de reële getallen, verschillend van 0 geldt dat a < b en c < d, welke van volgende beweringen zijn dan ook juist?
A) a - c < b - d, B) a - d < b - c, C) a.c < b.c, D) 1 / b < 1 / a.
3) Welke van volgende lijnen verdeelt een driehoek in twee even grote delen?
A) een hoogtelijn, B) een bissectrice van een hoek, C) een zwaartelijn,
E) een middelloodlijn van een zijde.
4) Ik beschouw de getallen 4, 8, 9, 16, 27, 32, 64, 81 en 243. Als ik telkens twee van deze getallen vermenigvuldig, hoeveel verschillende resultaten kan ik dan bekomen?

6)De helft van 8a / 12 is? A) 2a / 3, B) a / 3, C) 4a / 3, D) 4a / 24,
E) 4a / 6.
7) Een moderne voetbal is opgebouwd uit 12 vijfhoeken en 20 zeshoeken. Hoeveel ribben telt de bal?
8 ) Hoe kun je tien bomen planten zodat je vijf rijen van vier bomen ziet?
9) Kamelixen hebben 3 keer meer bulten dan dromedixen. Een gemengde kudde van 24 dieren heeft samen evenveel bulten als 10 dromedixen en 6 kamelixen samen. Hoeveel dromedixen zijn er in de kudde?

11) De moeder van David en Sofie is in verwachting van een baby. Als het een meisje wordt heeft David tweemaal zoveel zussen als broers; als het een jongen wordt heeft Sofie tweemaal zoveel broers als zussen. Hoeveel kinderen heeft moeder ... de toekomstige baby niet meegerekend?
12 ...een moeilijke ... tracht 21 te bekomen door 1, 5, 6 en 7 ieder éénmaal te gebruiken en verder alleen met de bewerkingen optellen, aftrekken, vermenigvuldigen en delen.te werken. Let op: de bewerkingen moeten niet noodzakelijk allemaal voorkomen. Prutswerk ...


15) De diagonalen van een ruit hebben als lengten 3 en 7,20 meter. De afstand tussen de evenwijdige zijden is dan gelijk aan ?
A) 12 / 5, B) 36 /13, C) 18 / 13, D) 72 / 13, E) 36 / 17
tot daar een langere afsluiter,
rustig aan en veel succes,
denook