Wiskundige problemen en probleempjes 2
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Goede avond Denook en alle anderen
Vraag 2. Een klein schaakbord telt 4 x 4 vierkantjes.
Hoeveel vierkanten kan je aanwijzen op het bord?
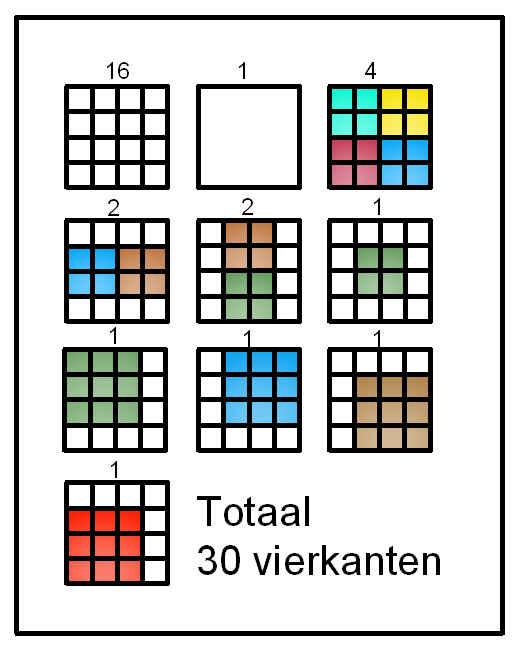
1 vierkant van 16 vierkantjes.
16 vierkanten van 1 vierkantje.
4 vierkanten van 4 vierkantjes.
2 vierkanten van 4 vierkantjes in het midden van het bord van boven naar beneden.
2 vierkanten van 4 vierkantjes in het midden van het bord van links naar rechts.
1 vierkant van 4 vierkantjes in het midden.
4 vierkanten van 9 vierkantjes.
Antwoord: 30 vierkantjes.
Vraag 2. Een klein schaakbord telt 4 x 4 vierkantjes.
Hoeveel vierkanten kan je aanwijzen op het bord?
1 vierkant van 16 vierkantjes.
16 vierkanten van 1 vierkantje.
4 vierkanten van 4 vierkantjes.
2 vierkanten van 4 vierkantjes in het midden van het bord van boven naar beneden.
2 vierkanten van 4 vierkantjes in het midden van het bord van links naar rechts.
1 vierkant van 4 vierkantjes in het midden.
4 vierkanten van 9 vierkantjes.
Antwoord: 30 vierkantjes.
Sudoku, wijntjes proeven, genieten.
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goede avond allemaal
Vraag 9
ABCD 2401 mm²

Groetjes
Sloeber
Vraag 9
ABCD 2401 mm²

Groetjes
Sloeber
Meten is weten - Carpe diem
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
't Is just Pastoor
Groetjes
Sloeber

Groetjes
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Variante op de oplossing van Sloeber. (Vraag 9)
Zijde van vierkant DOPQ = 12. Zijde van vierkant EFGH = 35
Als men de oppervlakte van driehoek EDH kent, dan kent men de oppervlakte van ABCD. (opp. EFGH + 4 * (opp. EDH))
Berekening van OE.
Driehoek OEP en driehoek DEH zijn gelijkvormig.
(OE/ED) = (EP/EH) of (OE/(OE + 12)) = EP/35.
EP = (35 * OE)/(OE + 12). (1).
Driehoek OEP (Pythagoras)
EP² = OE² + 12².
EP = √(OE² + 144) (2).
(2) = (1).
(35 * OE)/(OE + 12) = √(OE² + 144)
Kwadrateren: (1225 * OE²)/(OE² + 144 + (24 * OE)) = OE² + 144
of ((OE)²)² + 24 OE³ – 937 OE² + 3456 OE +1442 = 0
Vierdegraad vergelijking,
empirisch berekend met 10, 20, 15, 17, en 16 was juist.
OE = 16 en DE = 28.
Berekening van EP.
Pythagoras in driehoek OEP
EP² = 16² + 12² = 400
EP = 20 en PH = 15.
Berekening van QH.
Pythagoras in driehoek QPH.
PH² = 225 = QH² + 12²
QH = 9 en DH = 21.
De oppervlakte van ABCD.
1225 + 4 * (oppervlakte van driehoek EDH).
Of 1225 + 4((28 * 21)/2) = 1225 + 1176 =
2401.
Zijde van vierkant DOPQ = 12. Zijde van vierkant EFGH = 35
Als men de oppervlakte van driehoek EDH kent, dan kent men de oppervlakte van ABCD. (opp. EFGH + 4 * (opp. EDH))
Berekening van OE.
Driehoek OEP en driehoek DEH zijn gelijkvormig.
(OE/ED) = (EP/EH) of (OE/(OE + 12)) = EP/35.
EP = (35 * OE)/(OE + 12). (1).
Driehoek OEP (Pythagoras)
EP² = OE² + 12².
EP = √(OE² + 144) (2).
(2) = (1).
(35 * OE)/(OE + 12) = √(OE² + 144)
Kwadrateren: (1225 * OE²)/(OE² + 144 + (24 * OE)) = OE² + 144
of ((OE)²)² + 24 OE³ – 937 OE² + 3456 OE +1442 = 0
Vierdegraad vergelijking,
empirisch berekend met 10, 20, 15, 17, en 16 was juist.
OE = 16 en DE = 28.
Berekening van EP.
Pythagoras in driehoek OEP
EP² = 16² + 12² = 400
EP = 20 en PH = 15.
Berekening van QH.
Pythagoras in driehoek QPH.
PH² = 225 = QH² + 12²
QH = 9 en DH = 21.
De oppervlakte van ABCD.
1225 + 4 * (oppervlakte van driehoek EDH).
Of 1225 + 4((28 * 21)/2) = 1225 + 1176 =
2401.
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
we zijn weer drie vragen verder,
vraag 6) - lotte - ok, maar ...
- je geeft het antwoord 100% correct,
- een tijdje later verander je ... fout nu,
- nog een tijdje later weer de eerste versie ... juist natuurlijk,
welke duistere krachten spelen door je hoofd?
vraag 2) - pastoor - ok,
mooi geïllustreerd ook door sloeberkebebo
en dan vraag 9)
- sloeberkebebo tekent en meet en bekomt 2401 mm²
- pastoor gooit er een lang bewijs tegenaan en vindt ook 2401 mm².
- een andere benadering (iets eenvoudiger dan bij pastoor):
we stellen de lengte van ED = a en deze van DH = b,
dan is de oppervlakte van driehoek EDH = a.b/2 (1)
nu is deze oppervlakte ook gelijk aan: 144 + (a-12).12/2 + (b-12).12/2
uitgerekend .... 6.(a + b) (2)
(1) = (2) geeft dan
opp driehoek EDH = ab/2 = 6.(a + b) of ab = 12.(a + b),
opp vier driehoeken: 2.ab = 24.(a + b)
we zijn er bijna, want a + b is ook de zijde van het grote vierkant.
Daarom
opp ABCD = ( a + b)² = 1225 + 24.(a + b)
stellen we a+b = x, dan krijgen we een vierkantsvergelijking:
x² - 24x - 1225 = 0
Hiervan zijn de oplossingen 49 en (-25), hier niet bruikbaar.
Besluit: a + b = 49 en opp ABCD = 49² = 2401
blijven over:
vraag 3), denk eraan voor iedere zijde (ribbe) van het veelvlak (in de
ruimte) heb je twee zijden van de veelhoeken nodig, die bij elkaar komen
vraag 5), als een getal deelbaar is door 9 is de som der cijfers ook deel-
baar door 9 en de nieuwe som der cijfers ook deelbaar door 9, ... enz
vraag 8 ), is een weggevertje ... had hier al troontje verwacht.
tot morgen,
denook
we zijn weer drie vragen verder,
vraag 6) - lotte - ok, maar ...
- je geeft het antwoord 100% correct,
- een tijdje later verander je ... fout nu,
- nog een tijdje later weer de eerste versie ... juist natuurlijk,
welke duistere krachten spelen door je hoofd?
vraag 2) - pastoor - ok,
mooi geïllustreerd ook door sloeberkebebo
en dan vraag 9)
- sloeberkebebo tekent en meet en bekomt 2401 mm²
- pastoor gooit er een lang bewijs tegenaan en vindt ook 2401 mm².
- een andere benadering (iets eenvoudiger dan bij pastoor):
we stellen de lengte van ED = a en deze van DH = b,
dan is de oppervlakte van driehoek EDH = a.b/2 (1)
nu is deze oppervlakte ook gelijk aan: 144 + (a-12).12/2 + (b-12).12/2
uitgerekend .... 6.(a + b) (2)
(1) = (2) geeft dan
opp driehoek EDH = ab/2 = 6.(a + b) of ab = 12.(a + b),
opp vier driehoeken: 2.ab = 24.(a + b)
we zijn er bijna, want a + b is ook de zijde van het grote vierkant.
Daarom
opp ABCD = ( a + b)² = 1225 + 24.(a + b)
stellen we a+b = x, dan krijgen we een vierkantsvergelijking:
x² - 24x - 1225 = 0
Hiervan zijn de oplossingen 49 en (-25), hier niet bruikbaar.
Besluit: a + b = 49 en opp ABCD = 49² = 2401
blijven over:
vraag 3), denk eraan voor iedere zijde (ribbe) van het veelvlak (in de
ruimte) heb je twee zijden van de veelhoeken nodig, die bij elkaar komen
vraag 5), als een getal deelbaar is door 9 is de som der cijfers ook deel-
baar door 9 en de nieuwe som der cijfers ook deelbaar door 9, ... enz
vraag 8 ), is een weggevertje ... had hier al troontje verwacht.
tot morgen,
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goede avond allemaal
Vraag 3
Het is niet mogelijk
Groetjes
Sloeber
Vraag 3
Het is niet mogelijk
Groetjes
Sloeber
Meten is weten - Carpe diem
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Goede avond Denook en allemaal.
5) Gegeven: A, een natuurlijk getal, van 2010 cijfers en deelbaar door 9.
B, het getal bekomen door alle cijfers van A op te tellen.
C, het getal, bekomen door alle cijfers van B op te tellen.
D, het getal, bekomen door alle cijfers van C op te tellen.
Gevraagd: wat is de hoogste waarde die D kan aannemen?
Met allemaal 8 of 7 of 5 of 4 of 2 of 1 is het getal van 2010 cijfers niet deelbaar door 9.
Allemaal 9: B= 18090, C = 18, D = 9
Allemaal 6: B= 12060, C = 9, D = 9
Allemaal 3: B= 06030, C = 9, D = 9
Antwoord: D = 9.
(bij gebrek aan tijd deze week heb ik nog niet 100% nagekeken of een
veelvoud van 9 een oplossing is. Ben wel zeker dat D zijnde 63 of 54 geen oplossing levert. Van de rest weet ik het nog niet).
5) Gegeven: A, een natuurlijk getal, van 2010 cijfers en deelbaar door 9.
B, het getal bekomen door alle cijfers van A op te tellen.
C, het getal, bekomen door alle cijfers van B op te tellen.
D, het getal, bekomen door alle cijfers van C op te tellen.
Gevraagd: wat is de hoogste waarde die D kan aannemen?
Met allemaal 8 of 7 of 5 of 4 of 2 of 1 is het getal van 2010 cijfers niet deelbaar door 9.
Allemaal 9: B= 18090, C = 18, D = 9
Allemaal 6: B= 12060, C = 9, D = 9
Allemaal 3: B= 06030, C = 9, D = 9
Antwoord: D = 9.
(bij gebrek aan tijd deze week heb ik nog niet 100% nagekeken of een
veelvoud van 9 een oplossing is. Ben wel zeker dat D zijnde 63 of 54 geen oplossing levert. Van de rest weet ik het nog niet).
Sudoku, wijntjes proeven, genieten.
-
pastoor - Lid geworden op: 19 mar 2005, 21:55
- Locatie: Hoeselt, White House
Sloeber,
idem.
(Heb de volgende veelvlakken bekeken: regelmatig veelvlak, halfregelmatig veelvlak, Archimedes lichaam, Catalan lichaam, Johnson lichaam, Kepler-Poinsot lichaam en het sferisch lichaam en vindt nergens een oplossing). Antwoord: neen.
Wikipedia.
http://nl.wikipedia.org/wiki/Veelvlak
idem.
(Heb de volgende veelvlakken bekeken: regelmatig veelvlak, halfregelmatig veelvlak, Archimedes lichaam, Catalan lichaam, Johnson lichaam, Kepler-Poinsot lichaam en het sferisch lichaam en vindt nergens een oplossing). Antwoord: neen.
Wikipedia.
http://nl.wikipedia.org/wiki/Veelvlak
Sudoku, wijntjes proeven, genieten.
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
afronden ...
vraag 8 ) lotte - ok
was inderdaad een weggevertje - je had alleen een
zakrekenmachientje nodig dat een vierkantsworten kon geven,
vraag 3) sloeberkebebo en pastoor - ok
sloeberkebebo: "neen het gaat niet"
pastoor: ook "neen", met een ganse waslijst ruimtelichamen erbij.
Beste leerlingen, hier komen nooit problemen waar er 'hogere' wiskunde
voor nodig is; een beetje inzicht en nog wat parate kennis van de leerstof
tot vierde, soms vijfde jaar humaniora zou moeten volstaan.
De hint was hier: je hebt steeds van twee veelhoeken een zijde nodig
om tot een ribbe van het te maken ruimtelichaam te komen.
Welnu, als je de som maakt van de aantallen zijden van de gegeven
veelhoeken, vind je 43!! Een oneven getal ... dus gaat het NIET.
vraag 5) - pastoor - ok - alhoewel ...
jij gaat er van uit dat het getal geschreven wordt met eenzelfde cijfer ...
allemaal enen, allemaal tweeën, enz.
Neen, het is een getal, geschreven met 2010 cijfers, willekeurige cijfers,
willekeurige volgorde ... alleen is dat 'grote' getal deelbaar door 9.
Daarna is je redenering goed.
Als het allemaal 'negens' zijn, vinden we als som der cijfers 18090.
Dat is B; C is dan 18 en D is dan 9.
Zijn het niet allemaal 'negens' dan zal de som der cijfers kleiner zijn dan
18090 en zullen we voor D nog de waarde 9 vinden; ook al kan C dan
groter zijn dan 18.
Besluit: antwoord is steeds 9.
Dit was het weer,
volgende afspraak op dinsdag 7 december,
tot dan - opgelet voor de komende sneeuw ...
denook
afronden ...
vraag 8 ) lotte - ok
was inderdaad een weggevertje - je had alleen een
zakrekenmachientje nodig dat een vierkantsworten kon geven,
vraag 3) sloeberkebebo en pastoor - ok
sloeberkebebo: "neen het gaat niet"
pastoor: ook "neen", met een ganse waslijst ruimtelichamen erbij.
Beste leerlingen, hier komen nooit problemen waar er 'hogere' wiskunde
voor nodig is; een beetje inzicht en nog wat parate kennis van de leerstof
tot vierde, soms vijfde jaar humaniora zou moeten volstaan.
De hint was hier: je hebt steeds van twee veelhoeken een zijde nodig
om tot een ribbe van het te maken ruimtelichaam te komen.
Welnu, als je de som maakt van de aantallen zijden van de gegeven
veelhoeken, vind je 43!! Een oneven getal ... dus gaat het NIET.
vraag 5) - pastoor - ok - alhoewel ...
jij gaat er van uit dat het getal geschreven wordt met eenzelfde cijfer ...
allemaal enen, allemaal tweeën, enz.
Neen, het is een getal, geschreven met 2010 cijfers, willekeurige cijfers,
willekeurige volgorde ... alleen is dat 'grote' getal deelbaar door 9.
Daarna is je redenering goed.
Als het allemaal 'negens' zijn, vinden we als som der cijfers 18090.
Dat is B; C is dan 18 en D is dan 9.
Zijn het niet allemaal 'negens' dan zal de som der cijfers kleiner zijn dan
18090 en zullen we voor D nog de waarde 9 vinden; ook al kan C dan
groter zijn dan 18.
Besluit: antwoord is steeds 9.
Dit was het weer,
volgende afspraak op dinsdag 7 december,
tot dan - opgelet voor de komende sneeuw ...
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Voor de vragen van meester Denook

Tot vanavond .............

Tot vanavond .............
Meten is weten - Carpe diem
-
denook - Lid geworden op: 20 aug 2006, 13:25
- Locatie: Vlaams-Brabant
goede avond iedereen,
voorlaatste reeks wiskundige problemen en probleempjes van 2010,
1) Frieda en Tom verwachten een kindje. Ze willen 120 doosjes vullen
met telkens 30 suikerbonen. Maar als er 100 doosjes gevuld zijn, zijn
alle bonen op. Ze nemen nu uit de gevulde doosjes overal een zelfde
aantal bonen weg, om nieuwe doosjes te vullen, tot er overal evenveel
zijn. Hoeveel bonen moeten ze per doosje uit de eerste honderd doos-
jes zo wegnemen?
2) Hoeveel natuurlijke getallen, kleiner dan 222 zijn er, die bij deling door
8, rest 6 geven; bij deling door 6, rest 4 geven en bij deling door 4, rest
2 geven?
3) zie figuur sloeberkebebo:
ABCD is een vierkant met op AD een punt T.
Door B, een loodlijn op TC, die TC snijdt in P.
Als PC = 3 en BP = 4, dan is TD = ????
4) Op een cirkel liggen drie punten A, B en C, die de cirkel in drie gelijke
delen verdelen. Bereken de oppervlakte van driehoek ABC, als de straal
van de cirkel gelijk is aan 2 meter.
5) Een rechthoek met afmetingen b en c en een vierkant met zijde a heb-
ben gelijke oppervlakten. Wat is dan juist?
A) a-c = c-b, B) b+c = 2a, C) a/c = b, D) b.c = 1, E) c/a = a/b
6) In een klas van 24 leerlingen zijn er 21 die zwemmen, 18 spelen
schaak en 10 zingen in een koor. Eén leerling zit in de drie groepen.
Hoeveel schakers zingen in het koor?
7) zie figuur sloeberkebeo:
In een gelijbenige driehoek ABC, met top in A, is O het middelpunt van
de ingeschreven cirkel. Als de tophoek A = 48°, hoe groot is dan de
hoek BOC?
8 ) Hoeveel reële getallen m bestaan er waarvoor de vergelijkingen
x² + mx + 1 = 0 en x² + x + m = 0 minstens één gemeenschappelijke
oplossing hebben?
9) Een mannequin die op de catwalk loopt, weegt gekleed, 59 kilogram.
Naakt weegt ze 58 kilogram meer dan haar kleren.
Hoeveel wegen haar kleren dan wel?
10) DEZE VRAAG EN ANTWOORD BIJHOUDEN VOOR VOLGENDE REEKSEN.
In een klas met 13 leerlingen wil men een tennistornooi organiseren, met
alleen wedstrijden 'dubbel' ( = twee tegen twee -).
Hoeveel verschillende wedstrijden zijn er mogelijk als twee leerlingen
nooit willen meespelen?
weer een mooie mix van rekenen, meten, redeneren ...
succes iedereen,
tot morgen,
denook
voorlaatste reeks wiskundige problemen en probleempjes van 2010,
1) Frieda en Tom verwachten een kindje. Ze willen 120 doosjes vullen
met telkens 30 suikerbonen. Maar als er 100 doosjes gevuld zijn, zijn
alle bonen op. Ze nemen nu uit de gevulde doosjes overal een zelfde
aantal bonen weg, om nieuwe doosjes te vullen, tot er overal evenveel
zijn. Hoeveel bonen moeten ze per doosje uit de eerste honderd doos-
jes zo wegnemen?
2) Hoeveel natuurlijke getallen, kleiner dan 222 zijn er, die bij deling door
8, rest 6 geven; bij deling door 6, rest 4 geven en bij deling door 4, rest
2 geven?
3) zie figuur sloeberkebebo:
ABCD is een vierkant met op AD een punt T.
Door B, een loodlijn op TC, die TC snijdt in P.
Als PC = 3 en BP = 4, dan is TD = ????
4) Op een cirkel liggen drie punten A, B en C, die de cirkel in drie gelijke
delen verdelen. Bereken de oppervlakte van driehoek ABC, als de straal
van de cirkel gelijk is aan 2 meter.
5) Een rechthoek met afmetingen b en c en een vierkant met zijde a heb-
ben gelijke oppervlakten. Wat is dan juist?
A) a-c = c-b, B) b+c = 2a, C) a/c = b, D) b.c = 1, E) c/a = a/b
6) In een klas van 24 leerlingen zijn er 21 die zwemmen, 18 spelen
schaak en 10 zingen in een koor. Eén leerling zit in de drie groepen.
Hoeveel schakers zingen in het koor?
7) zie figuur sloeberkebeo:
In een gelijbenige driehoek ABC, met top in A, is O het middelpunt van
de ingeschreven cirkel. Als de tophoek A = 48°, hoe groot is dan de
hoek BOC?
8 ) Hoeveel reële getallen m bestaan er waarvoor de vergelijkingen
x² + mx + 1 = 0 en x² + x + m = 0 minstens één gemeenschappelijke
oplossing hebben?
9) Een mannequin die op de catwalk loopt, weegt gekleed, 59 kilogram.
Naakt weegt ze 58 kilogram meer dan haar kleren.
Hoeveel wegen haar kleren dan wel?
10) DEZE VRAAG EN ANTWOORD BIJHOUDEN VOOR VOLGENDE REEKSEN.
In een klas met 13 leerlingen wil men een tennistornooi organiseren, met
alleen wedstrijden 'dubbel' ( = twee tegen twee -).
Hoeveel verschillende wedstrijden zijn er mogelijk als twee leerlingen
nooit willen meespelen?
weer een mooie mix van rekenen, meten, redeneren ...
succes iedereen,
tot morgen,
denook
-
sloeberkebebo - Lid geworden op: 04 dec 2007, 13:51
- Locatie: Roeselare
Goede avond allemaal
Vraag 3
TD=3,75
BC=Wortel (4²+3²)=5
sinB=3/5=0,60...==>36,87°...
HoekB=hoekC
tanC=0,75...
TD=0,75...x5=3,75
Groetjes
Sloeberke

Vraag 3
TD=3,75
BC=Wortel (4²+3²)=5
sinB=3/5=0,60...==>36,87°...
HoekB=hoekC
tanC=0,75...
TD=0,75...x5=3,75
Groetjes
Sloeberke

Meten is weten - Carpe diem