Wiskundige problemen en probleempjes 2

[denook]

mag ik nog even vanavond -
we zijn er

vraag 6) lotte + sloeberkebebo + troontje -
iedereen ok!

vraag 9) sloeberkebebo - ook volledig ok

en dan ...
vraag 2) troontje ... ok ...
versta nu pas je redenering,
denook wordt oud,

groetjes en tot een volgende reeks,
zal dinsdag 8 februari zijn,

denook

[pastoor]

Variante op vraag 6.

Munten met het vlakke deel tegen mekaar. De munt van 1 euro heeft een dikte van 2,33 mm. 2.145.922 munten van 1 euro op een rij leveren 4,999998 km.

Munten met de zijrand tegen mekaar. De munt van 1 euro heeft een diameter van 23,25 mm. 215.053 munten van 1 euro op een rij vormen 4,999982 km.

Antwoord: 2.145.922 munten van 1 euro (munten met vlakke deel tegen mekaar).

[sloeberkebebo]

Dag allemaal

Ik denk dat pastoor de slimste is van ons allemaal ! Die legt ze natuurlijk op elkaar ! Daarom is het ook een pastoor , nietwaar ! Die is gewend om geld te tellen uit de offerblokken ........

Groetjes
Sloeber

[sloeberkebebo]

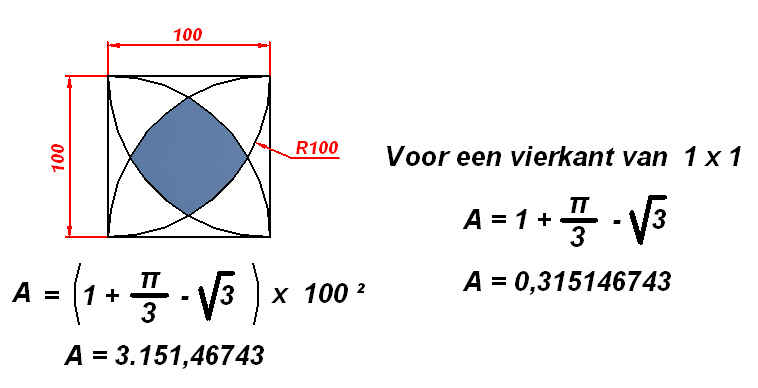
Een leuk tussendoortje

Bereken de oppervlakte van het gekleurde dedeelte .


Groetjes
Sloeber

[pastoor]

Dat is berekenbaar via berekeningen op het gearceerde deel.
Noem de hoekpunten van het gearceerde deel ABCD.
En teken de rechten AB, BC, CD en DA.
Dan is AB = BC = CD = DA, een vierkant.

Dan is de oppervlakte van het gearceerde deel =
de oppervlakte van het vierkant + 4*(oppervlakte van segment AB)
Segment AB bevat de boog AB en de rechte AB.

* * * * *

Oppervlakte van vierkant ABCD.
Teken twee rechten uit A naar beneden, een loodrecht en een naar de linkse hoek beneden.
Dat vormt een rechthoekige driehoek met:
(100) schuine zijde, (50) kleine rechthoekzijde
en de hoogte = √((100)² -(50)²) = 86,6.
De 86,6 is de diagonaal en het verlengde (100 -86,6 = 13,4) naar de zijde.
De diagonaal van het vierkant ABCD is dan 86,6 – 13,4 = 73,2.
Diagonaal 73,2 en zijde Z en Pythagoras: (73,2)² = 2.Z².
Opp van vierkant ABCD = (73,2)²/2 = 2679,12 cm².


Oppervlakte van segment AB.
Het segment bestaat uit een zijde AB (koorde) en de boog AB.
De sector bestaat uit de koorde AB en het middelpunt O van de cirkel.

K is de lengte van de koorde = AB = √(2679,12) cm = 51,76 cm
R is de straal van de cirkel = 100 cm.
L is de afstand van het middelpunt O van de cirkel tot de koorde.
L (Pythagoras) = √(R² - (K/2)²) = √(93,87) = 96,59 cm.
H is de hoogte van het segment = R – L = 100 – 96,59 = 3,41 cm.
Omega is de hoek gevormd door B en A te verbinden met het middelpunt van de cirkel.
S is de lengte van de cirkelboog = R * Omega.

Oppervlakte segment = oppervlakte sector – oppervlakte driehoek ABO.

Oppervlakte van de sector is de verhouding tussen de omtrek van de sector en de oppervlakte van de cirkel.
Oppervlakte van de sector: (S/2.pi.R) * (pi.R²) = 0,5*S*R
Met S=R*omega wordt de oppervlakte: 0,5*R²*omega = 5000*omega cm².

Oppervlakte driehoek ABO = (K*L)/2 = (51,76 * 96,59)/2 = 2499,75 cm².

Oppervlakte segment = 5000*omega cm² – 2499,75 cm²


Oplossing.
Opp gearceerd deel = 4*(oppervlakte segment) + oppervlakte vierkant.
4*(5000*omega - 2499,75) cm² + 2.679,12 cm².

Er blijft 1 onbekende.
Hoeveel is omega?
Nog rekenen.

[sloeberkebebo]

Rare vierhoek ......




Vele groetjes Sloeber ......

[sloeberkebebo]

Dag allemaal .

Dit is voor de vragen van meester Denook .

[denook]

dinsdag 8 februari 2011,

goede avond iedereen,
nieuwe reeks wiskundige problemen en proleempjes,

1) A en B vullen samen een container in 20 minuten,
B en C vullen hem samen in 30 minuten,
C en A vullen hem samen in 40 minuten.
In hoeveel tijd vult A alleen de container?

2) Op een schietschijf staan de getallen 16, 17, 23, 24 en 39.
Zoek het kleinste aantal schoten om precies de som 100 te bekomen.

3) geen wiskunde, maar toch een mooi 'zoek'vraagje ...
De 'canonieke vorm' van PAARD is AADPR
(dwz. de letters in alfabetische volgorde plaatsen).
ADEM, BEGIN, CHLOOR zijn woorden die in de canonieke vorm
niet meer veranderen.
Vind nog 3 woorden van minstens 5 letters die al in de canonieke vorm
staan.

4) zie tekening sloeberkebebo
ABCD is een vierkant met een zijde van 6 cm.
De diagonalen snijden elkaar in O.
P en Q verdelen AC in drie gelijke delen: AP, PQ en QC.
R, O en S verdelen BD in vier gelijke delen: BR, RO, OS en SD.
Bereken de oppervlakte van de vierhoek PRQS.

5) Een antiquair verkocht twee klokken, elk voor 480 euro.
Op de ene wint hij zo 20%; op de andere verliest hij 20%.
Maakt hij nu in totaal winst, verlies of geen van beiden?

6) Elsy heeft een aantal dieren,
2 dieren zijn geen zoogdieren,
3 dieren zijn geen honden,
4 dieren zijn geen katten,
5 dieren zijn geen papegaaien.
Hoeveel honden en hoeveel katten heeft Elsy?

7) Hoe kan je met planken van 3,80 m lang, 20 cm breed,
en planken van 3,60 m lang, 20 cm breed,
een kamer van 4 m op 4 m bevloeren, zonder één plank door te zagen?

8 ) zie tekening sloeberkebebo
AD is de middellijn van een halve cirkel met straal 2.
De punten B en C verdelen de halve cirkel in drie gelijke bogen.
Bereken de oppervlakte van de vierhoek ABCD.

9) Hoeveel priemgetallen zijn er die op twee verschillende manieren als
een som van zelf twee priemgetallen kunnen worden geschreven?
A) 0, B) 1, C) 2, D) 3, E) meer dan 3

10) een laatste keer onze klas tennissers ...
zie ook vragen 10 (-met de oplossingen-) van vorige reeksen vragen.
In een klas van 13 leerlingen wil men een tennistornooi organiseren met
alleen 'dubbel'-spelen (= twee tegen twee).
Hoeveel verschillende wedstrijden zijn er mogelijk als twee leerlingen
alleen samen ploeg willen vormen en twee andere leerlingen niet samen
op het terrein willen staan? ... mooi om te eindigen ...

Dit was het dan weer,
dank aan sloeberkebebo voor de mooie figuren,
succes iedereen,
tot morgen, denook

[pastoor]

Goede avond Denook

vraag 2
4 * 17 en 2 * 16 = 100
Of 6 maal schieten.

[sloeberkebebo]

Goede avond allemaal

Vraag 8

Vierhoek ABCD bestaat uit 3 gelijkzijdige driehoeken met een zijde van 2
De oppervlakte van een gelijkzijdige driehoek is
( 2² * sin60°)/2 = 1,73.... of W3
De oppervlakte van vierhoek ABCD is dus 1,73.... * 3 = 5,196152424..

Groetjes
Sloeber

[lotte]

Goeie avond denook

vraag 3

Aders
Borst
Chips

Groetjes
lotte.

[troontje]

Goede morgen iedereen,

vraag1)


A=15 min + B= 5 min (samen 20 min)
B= 5 min + C= 25 min (samen 30 min)
C=25 min + A=15min (samen 40 min)

15+5+25=45:3=15min x 2=30 min

A vult de container alleen in 30 min


troontje

[denook]

goede avond iedereen,
vier antwoorden
en tweehonderdennegen aanklikkers later,
eerste evaluatie

vraag 2) pastoor ok

vraag 8 ) sloeberkebebo - ok

vraag 3) lotte - ok

vraag 1) troontje - niet ok,
opgave verkeerd geïnterpreteerd,
alhoewel de tekst vrij duidelijk was ...

'A en B vullen samen een container in 20 minuten'

dat betekent dat A en B samen beginnen laden,
de ene werkt vlugger dan de andere,
doch ze blijven elk 20 minuten werken,
en dan is de container vol.

zijn dus opgelost: vragen 2, 3 en 8

tot morgen, denook

[pastoor]

Goede avond Denook en de anderen.

4) ABCD is een vierkant met een zijde van 6 cm. De diagonalen snijden elkaar in O. P en Q verdelen AC in drie gelijke delen: AP, PQ en QC. R, O en S verdelen BD in vier gelijke delen: BR, RO, OS en SD. Bereken de oppervlakte van de vierhoek PRQS.

De diagonaal van vierkant ABCD is = √(6² + 6²) = √72.
PO = OQ = (√72)/6 en RO = SO = (√72)/4

Opp. PRO = opp. RQO = opp. OQS = opp. POS.
Opp. PRO = (RO * PO)/2 = ((√72)/4 * (√72)/6)/2 = (72/24)/2= 1,5 cm².

Antwoord: opp. PRQS = 4 * 1,5 cm² = 6 cm²

[pastoor]

1) A en B vullen samen een container in 20 minuten, B en C vullen hem samen in 30 minuten, C en A vullen hem samen in 40 minuten. In hoeveel tijd vult A alleen de container?

Opgave.
A 20 minuten + B 20 minuten = 1 container.
B 30 minuten + C 30 minuten = 1 container.
C 40 minuten + A 40 minuten = 1 container.

Op gelijke minuten brengen.
A 30 minuten + B 30 minuten = 1,5 container.(1)
B 30 minuten + C 30 minuten = 1 container. (2)
C 30 minuten + A 30 minuten = 0,75 container. (3)

A wordt gevonden via (1) – (2) + (3):
A 60 minuten = 1, 25 container.
A 48 minuten = 1 container.
A 20 minuten = 0,41666666 container.

Antwoord A vult een container in 48 minuten.

* * *

Ter info:

B wordt gevonden via (1) + (2) – (3):
B 60 minuten = 1, 75 container.
B 34,2857142948 minuten = 1 container.
B 20 minuten = 0,58333333 container

B 20 minuten + A 20 minuten = 0,41666.. + 0,58333.. = 1 container.